
| A. | 0<m≤1 | B. | 0≤m≤1 | C. | 0<m<1 | D. | 0≤m<1 |
分析 根据题意得出对任意实数x,mx2-6mx+m+8≥0恒成立,讨论m的取值,
求出满足条件的m的取值范围即可.
解答 解:∵函数y=$\sqrt{m{x}^{2}-6mx+m+8}$的定义域是R,
∴对任意实数x,mx2-6mx+m+8≥0恒成立,
当m=0时,不等式化为8≥0恒成立,
当m≠0时,要使对任意实数x,mx2-6mx+m+8≥0恒成立,
则$\left\{\begin{array}{l}{m>0①}\\{3{6m}^{2}-4m(m+8)≤0②}\end{array}\right.$,
解②得:0≤m≤1;
∴该不等式组的解集为(0,1],
综上,函数y=$\sqrt{m{x}^{2}-6mx+m+8}$的定义域是R时实数m的取值范围是0≤m≤1.
故选:B.
点评 本题考查了函数的定义域及其求法,也考查了分类讨论的数学思想,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
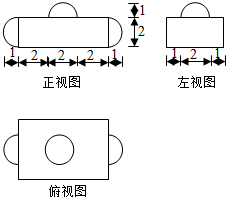
| A. | $48+\frac{4}{3}π$ | B. | 48+2π | C. | $48+\frac{8}{3}π$ | D. | 48+3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (0,4] | C. | $(0,\frac{1}{4}]$ | D. | $[\frac{1}{4},4]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{161}{29}$ | B. | $\frac{161}{31}$ | C. | $\frac{81}{15}$ | D. | $\frac{80}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
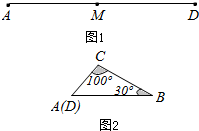 如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )
如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )| A. | 点M在AB上 | |
| B. | 点M在BC的中点处 | |
| C. | 点M在BC上,且距点B较近,距点C较远 | |
| D. | 点M在BC上,且距点C较近,距点B较远 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com