
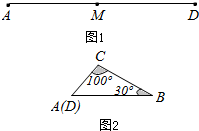
 如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )
如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )| A. | 点M在AB上 | |
| B. | 点M在BC的中点处 | |
| C. | 点M在BC上,且距点B较近,距点C较远 | |
| D. | 点M在BC上,且距点C较近,距点B较远 |
分析 根据钝角三角形中钝角所对的边最长可得AB>AC,取BC的中点E,求出AB+BE>AC+CE,再根据三角形的任意两边之和大于第三边得到AB<$\frac{1}{2}$AD,从而判定AD的中点M在BE上.
解答 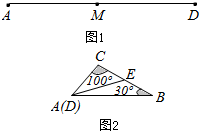 解:∵∠C=100°,
解:∵∠C=100°,
∴AB>AC,
如图,取BC的中点E,则BE=CE,
∴AB+BE>AC+CE,
由三角形三边关系,AC+BC>AB,
∴AB<$\frac{1}{2}$AD,
∴AD的中点M在BE上,
即点M在BC上,且距点B较近,距点C较远.
故选:C.
点评 本题考查了三角形的三边关系,作辅助线把△ABC的周长分成两个部分是解题的关键,本题需要注意判断AB的长度小于AD的一半,这也是容易忽视而导致求解不完整的地方.


科目:高中数学 来源: 题型:选择题

| A. | 72一$\frac{9π}{2}$ | B. | 72-4π | C. | 72一$\frac{7π}{2}$ | D. | 72-3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m≤1 | B. | 0≤m≤1 | C. | 0<m<1 | D. | 0≤m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{9}{4}$) | B. | (-∞,-$\frac{9}{4}$] | C. | [-$\frac{9}{4}$,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1+\sqrt{5}}{2}$,+∞) | B. | (1,1+$\sqrt{3}$) | C. | ($\frac{1+\sqrt{5}}{2}$,1+$\sqrt{3}$) | D. | ($\frac{1+\sqrt{5}}{2}$,2)∪(2,1+$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>0 | B. | a+b<0 | C. | a+b=0 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com