
分析 导数的运算法则和复合函数求导法则求导即可.
解答 解:f(x)=ln$\root{3}{x+1}$-$\frac{1}{3}$ln$\frac{1}{{x}^{2}-x+1}$,
∴f′(x)=$\frac{1}{\root{3}{x+1}}$•($\root{3}{x+1}$)′-$\frac{1}{3}$(x2-x+1)($\frac{1}{{x}^{2}-x+1}$)′
=$\frac{1}{\root{3}{x+1}}$•$\frac{1}{3}$(x+1)${\;}^{-\frac{2}{3}}$+$\frac{1}{3}$(x2-x+1)$\frac{2x-1}{({x}^{2}-x+1)^{2}}$;
=$\frac{1}{3}$•$\frac{1}{x+1}$+$\frac{1}{3}$•$\frac{2x-1}{{x}^{2}-x+1}$,
=$\frac{1}{3}$•$\frac{3{x}^{2}}{{x}^{3}+1}$,
=$\frac{{x}^{2}}{{x}^{3}+1}$.
故答案为:$\frac{{x}^{2}}{{x}^{3}+1}$.
点评 本题考查了导数的运算法则和复合函数求导法则,以及运算能力,属于基础题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2015)∪(2015,+∞) | B. | (-∞,-2015)∪(0,2015) | C. | (-2015,0)∪(0,2015) | D. | (-2015,0)∪(2015,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
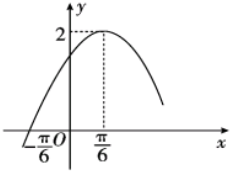 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |PF1|+|PF2|≥10 | B. | |PF1|+|PF2|≤10 | C. | |PF1|+|PF2|>10 | D. | |PF1|+|PF2|<10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,$\frac{π}{4}$] | C. | [$\frac{π}{4}$,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0≤x<2} | C. | {x|-1<x≤3} | D. | {x|2<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com