在棱长为a的正方体ABCD-A1B1C1D1,E、F分别为BC与A1D1的中点,
(1)求直线A1C与DE所成的角;
(2)求直线AD与平面B1EDF所成的角;
(3)求面B1EDF 与 面ABCD所成的角.
【答案】
分析:(1)在平面ABCD内,过C作CP∥DE交直线AD于P,则∠A
1CP(或补角)为异面直线A
1C与DE所成的角,在△A
1CP中,利用余弦定理,即可求得异面直线A
1C与DE所成的角;
(2)证明直线AD与平面B
1EDF所成的角为∠ADB
1,在直角△B
1AD中,利用余弦定理,即可求得直线AD与平面B
1EDF所成的角;
(3)连接EF、B
1D,交于点O,作OH⊥平面ABCD,作HM⊥DE,垂足为M,连接OM,则可得∠OMH为面B
1EDF 与 面ABCD所成的角,在直角△OHM中,利用正弦函数,即可求得面B
1EDF 与 面ABCD所成的角.
解答:
解:(1)如图,在平面ABCD内,过C作CP∥DE交直线AD于P,则∠A
1CP(或补角)为异面直线A
1C与DE所成的角
在△A
1CP中,A
1C=

a,CP=DE=

,A
1P=

∴cos∠A
1CP=

=

∴异面直线A
1C与DE所成的角为arccos

;
(2)∵平面ADE⊥平面ADF
∴AD在平面B
1EDF内的射影在∠EDF的平分线上,而四边形B
1EDF是菱形

∴DB
1为∠EDF的平分线
∴直线AD与平面B
1EDF所成的角为∠ADB
1.
在直角△B
1AD中,AD=a,AB
1=

a,B
1D=
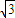
a,
∴cos∠ADB
1=

=

∴直线AD与平面B
1EDF所成的角为arccos

;
(3)连接EF、B
1D,交于点O,显然O为B
1D的中点,从而O为正方体的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心
作HM⊥DE,垂足为M,连接OM,则OM⊥DE,故∠OMH为面B
1EDF与面ABCD所成的角.

在直角△DOE中,OE=

,OD=

,DE=

则由面积关系可得OM=

在直角△OHM中,sin∠OMH=

=

∴面B
1EDF与面ABCD所成的角为arcsin
 点评:
点评:本题考查线线角、线面角、面面角,解题的关键是正确作出空间角,并在具体三角形中,利用余弦定理求出相应的角,属于中档题.

 解:(1)如图,在平面ABCD内,过C作CP∥DE交直线AD于P,则∠A1CP(或补角)为异面直线A1C与DE所成的角
解:(1)如图,在平面ABCD内,过C作CP∥DE交直线AD于P,则∠A1CP(或补角)为异面直线A1C与DE所成的角 a,CP=DE=
a,CP=DE= ,A1P=
,A1P=
 =
=
 ;
;
 a,B1D=
a,B1D=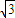 a,
a, =
=
 ;
;
 ,OD=
,OD= ,DE=
,DE=

 =
=



