
分析 (1)判断数列的第二项,然后求解通项公式即可.
(2)利用裂项法化简求解即可.
解答 解:(1)由a1=2,a2为整数知,且a3∈[3,5].
a3=4,{an}的通项公式为an=n+1.
(2)${b_n}=\frac{1}{(n+1)(n+3)}=\frac{1}{2}(\frac{1}{n+1}-\frac{1}{n+3})$,
于是${T_n}={b_1}+{b_2}+…+{b_n}=\frac{1}{2}(\frac{1}{2}+\frac{1}{3}-\frac{1}{n+2}-\frac{1}{n+3})=\frac{5}{12}-\frac{2n+5}{2(n+2)(n+3)}$.
点评 本题考查数列的判断以及数列求和,裂项法的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 不全相等 | B. | 均不相等 | C. | 都相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
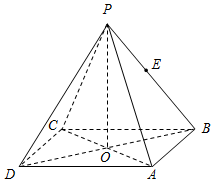 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (0,$\frac{1}{16}$) | D. | ($\frac{1}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com