
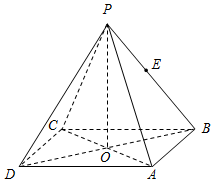
 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{\sqrt{6}}{2}$.分析 (1)取AD中点M,连接MO,PM,由正四棱锥的性质知∠PMO为所求二面角P-AD-O的平面角,∠PAO为侧棱PA与底面ABCD所成的角,则tan∠PAO=$\frac{\sqrt{6}}{2}$,设AB=a,则AO=$\frac{\sqrt{2}}{2}$a,PO=AO•tan∠POA=$\frac{\sqrt{3}}{2}$a,MO=$\frac{1}{2}$a,tan∠PMO=$\sqrt{3}$,∠PMO=60°;
(2)依题意连结AE,OE,则OE∥PD,故∠OEA为异面直线PD与AE所成的角,由正四棱锥的性质易证OA⊥平面POB,故△AOE为直角三角形,OE=$\frac{1}{2}$PD=$\frac{1}{2}$$\sqrt{P{O}^{2}+D{O}^{2}}$=$\frac{\sqrt{5}}{4}$a,所以tan∠AEO=$\frac{AO}{EO}$=$\frac{2\sqrt{10}}{5}$;
(3)延长MO交BC于N,取PN中点G,连BG,EG,MG,易得BC⊥平面PMN,故平面PMN⊥平面PBC,而△PMN为正三角形,易证MG⊥平面PBC,取MA的中点F,连EF,则四边形MFEG为平行四边形,从而MG∥FE,EF⊥平面PBC,F是AD的4等分点,靠近A点的位置.
解答 解:(1)取AD中点M,连接MO,PM,
依条件可知AD⊥MO,AD⊥PO,则∠PMO为所求二面角P-AD-O的平面角.
∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∴tan∠PAO=$\frac{\sqrt{6}}{2}$,
设AB=a,AO=$\frac{\sqrt{2}}{2}$a,
∴PO=AO•tan∠POA=$\frac{\sqrt{3}}{2}$a,
tan∠PMO=$\frac{PO}{MO}$=$\sqrt{3}$.
∴∠PMO=60°. 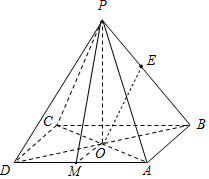
(2)连接AE,OE,
∵OE∥PD,
∴∠OEA为异面直线PD与AE所成的角.
∵AO⊥BD,AO⊥PO,
∴AO⊥平面PBD.
又OE?平面PBD,
∴AO⊥OE.
∵OE=$\frac{1}{2}$PD=$\frac{1}{2}$$\sqrt{P{O}^{2}+D{O}^{2}}$=$\frac{\sqrt{5}}{4}$a,
∴tan∠AEO=$\frac{AO}{EO}$=$\frac{2\sqrt{10}}{5}$;
(3)延长MO交BC于N,取PN中点G,连BG,EG,MG.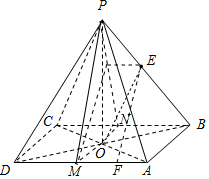
∵BC⊥MN,BC⊥PN,
∴BC⊥平面PMN
∴平面PMN⊥平面PBC.
又PM=PN,∠PMN=60°,
∴△PMN为正三角形.
∴MG⊥PN.又平面PMN∩平面PBC=PN,
∴MG⊥平面PBC.
∴F是AD的4等分点,靠近A点的位置.
点评 本题考查二面角及平面角的求法,异面直线所成角的正切值的求法,难度较大,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0或x>1} | B. | {x|0<x<1} | C. | {x|x<-1或x>0} | D. | {x|-1<x<0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com