
函数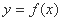 为定义在
为定义在 上的减函数,函数
上的减函数,函数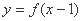 的图像关于点(1,0)对称,
的图像关于点(1,0)对称, 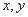 满
满
足不等式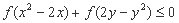 ,
, ,
,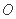 为坐标原点,则当
为坐标原点,则当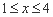 时,
时,
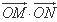 的取值范围为 ( )
的取值范围为 ( )
A.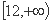 B.
B.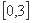 C.
C.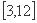 D.
D.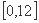
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
已知△ABC的面积S满足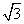 ≤S≤3,且
≤S≤3,且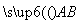 ·
·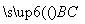 =6,设
=6,设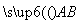 与
与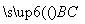 的夹角为θ.
的夹角为θ.
(1)求θ的取值范围;
(2)求函数f(θ)=sin2θ+2sin θ·cos θ+3cos2θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
为了考察两个变量 和
和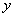 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量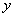 的观测数据的平均值都是
的观测数据的平均值都是 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 和
和 有交点
有交点 B.
B. 与
与 相交,但交点不一定是
相交,但交点不一定是
C. 与
与 必定平行 D.
必定平行 D. 与
与 必定重合
必定重合
查看答案和解析>>
科目:高中数学 来源: 题型:
某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com