
 +y2=1相交A、B两点,点C是椭圆上的动点,则△ABC面积的最大值为________.
+y2=1相交A、B两点,点C是椭圆上的动点,则△ABC面积的最大值为________.
 +y2=1联立,消元可得
+y2=1联立,消元可得 ,∴x=±
,∴x=±
 ,
, ),B(-
),B(- ,-
,- )
)
 +y2=1,消元可得3y2-2cy+c2-2=0
+y2=1,消元可得3y2-2cy+c2-2=0 
 =
=
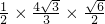 =
=



 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2010年单元测试卷(5)(解析版) 题型:解答题
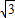 y-
y- =0与椭圆Γ交于A、B两点,|AB|=2,且∠AOB=
=0与椭圆Γ交于A、B两点,|AB|=2,且∠AOB=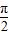 .
.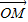 •
•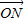 =0,求|MN|的最小值.
=0,求|MN|的最小值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省济南外国语学校高三(下)3月质量检测数学试卷(文科)(解析版) 题型:解答题
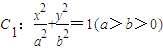 的离心率为
的离心率为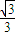 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.查看答案和解析>>
科目:高中数学 来源:2009年湖北省武汉市高三二月调考数学试卷(文理合卷)(解析版) 题型:解答题
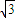 y-
y-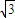 =0与椭圆Γ交于A、B两点,|AB|=2,且∠AOB=
=0与椭圆Γ交于A、B两点,|AB|=2,且∠AOB=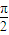 .
. •
•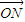 =0,求|MN|的最小值.
=0,求|MN|的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com