
如图所示, 是正三角形,
是正三角形, 和
和 都垂直于平面
都垂直于平面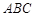 ,且
,且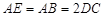 ,
,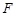 是
是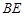 的中点.
的中点.
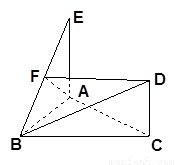
求证:(1) 平面
平面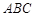 ;
;
(2)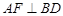 .
.
(1)根据题意,取AB中点N,连接FN、NC;又F为BE的中点 ∴FN为 的中位线,那么FN∥AE,进而得到平行性,AE∥CD,得到结论。
的中位线,那么FN∥AE,进而得到平行性,AE∥CD,得到结论。
(2)对于已知中,由于AE="AB" F是BE的中点 在 中N是AB的中点 ∴AF⊥BE
CN⊥AB,那么根据线面垂直的性质定理来的得到结论。
中N是AB的中点 ∴AF⊥BE
CN⊥AB,那么根据线面垂直的性质定理来的得到结论。
【解析】
试题分析:证明:(1)取AB中点N,连接FN、NC;又F为BE的中点 ∴FN为 的中位线, ∴FN∥AE FN=
的中位线, ∴FN∥AE FN= AE 又AE、CD都垂直与面ABC,2CD=AE ∴AE∥CD ∴ CD∥FN且CD=FN
AE 又AE、CD都垂直与面ABC,2CD=AE ∴AE∥CD ∴ CD∥FN且CD=FN
∴四边形CDFN为平行四边形 ∴DF∥CN 又CN 面ABC ∴ DF∥面ABC
面ABC ∴ DF∥面ABC
(2)∵AE="AB" F是BE的中点 在 中N是AB的中点 ∴AF⊥BE
CN⊥AB
中N是AB的中点 ∴AF⊥BE
CN⊥AB
∵AE⊥面ABC AE 面ABE ∴面ABE⊥面ABC 又CN⊥AB ∴CN⊥面ABE
面ABE ∴面ABE⊥面ABC 又CN⊥AB ∴CN⊥面ABE
∴ DF⊥面ABE ∴ DB在平面ABE的射影为BF ∴ AF⊥BD
考点:平行和垂直的证明
点评:主要是考查了熟练的运用中位线来证明平行和线面垂直的性质定理的运用,属于基础题。


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:2012-2013学年广东省韶关市高三第一次调研测试数学理科试卷(解析版) 题型:选择题
某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是正三角形),根据图中标出的数据,可得这个几何体的表面积为( )
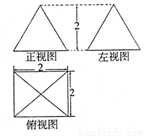
A.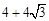 B.
B.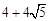 C.
C.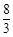 D.12
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com