
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
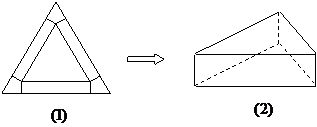
把边长为a的等边三角形铁皮如图(1)剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的底面为正三角形的直棱柱形容器(不计接缝)如图(2),设容器的高为x,容积为![]() 。
。
(Ⅰ)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕头市高三上学期期中文科数学试卷(解析版) 题型:选择题
设底面为正三角形的直棱柱体积为V,那么表面积最小时,底面边长为 ( )
A.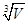 B.
B.
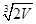 C.
C. 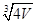 D. 2
D. 2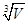
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com