练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知集合N={x|$\frac{1}{2}$＜2x+1＜4，x∈R}，M={x|x2+3x+2≤0，x∈R}，则M∩N（　　）
    A．（-2，1）B．（-2，-1）C．（-2，-1]D．[-2，-1]

    分析 求出M与N中不等式的解集，分别确定出两集合，求出两集合的交集即可．

    解答 解：由M中不等式变形得：（x+1）（x+2）≤0，
    解得：-2≤x≤-1，即M=[-2，-1]，
    由N中不等式变形得：2-1＜2x+1＜22，即-1＜x+1＜2，
    解得：-2＜x＜1，即N=（-2，1），
    则M∩N=（-2，-1]，
    故选：C．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河北沧州市高三9月联考数学（理）试卷（解析版） 题型：填空题

    在一次连环交通事故中，只有一个人需要负主要责任，但在警察询问时，甲说：“主要责任在乙”；乙说：“丙应负主要责任”；丙说“甲说的对”；丁说：“反正我没有责任”．四人中只有一个人说的是真话，则该事故中需要负主要责任的人是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．为了得到函数y=$\frac{1}{2}$sin（2x-$\frac{π}{3}$）的图象，只需将函数y=sinxcosx的图象（　　）
    A．向左平移$\frac{π}{3}$个单位B．向右平移$\frac{π}{3}$个单位
    C．向左平移$\frac{π}{6}$个单位D．向右平移$\frac{π}{6}$个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．正项等比数列{an}满足：a3=a2+2a1，若存在am，an，使得am•an=64a${\;}_{1}^{2}$，则$\frac{1}{m}$+$\frac{9}{n}$的最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=1+$\frac{2x+sinx}{{{x^2}+1}}$，若f（x）的最大值和最小值分别为M和N，则M+N等于（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．（1-x）（1+x）6的展开式中x3系数为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知集合M={0，1，2，5，6，7}，N={2，3，5，7}，若P=M∩N，则P的真子集个数为（　　）
    A．5B．6C．7D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知{an}是公差为3的等差数列，数列{bn}满足b1=1，b2=$\frac{1}{3}$，anbn+1+bn+1=nbn．
    （I）求数列{an}，{bn}的通项公式；
    （II）记cn=an•bn，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

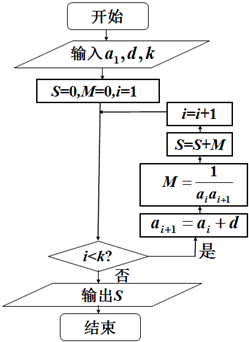    18．数列{an}的各项全为正数，且在如图所示的算法框图图中，已知输入k=2时，输出$S=\frac{1}{3}$；输入k=5时，输出$S=\frac{4}{9}$．
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）若${b_n}={2^{a_n}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    同步练习册答案