
分析 (I)利用递推关系可得a1.利用等差数列与等比数列的通项公式即可得出an,bn.
(II)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(Ⅰ)由数列{bn}满足b1=1,b2=$\frac{1}{3}$,anbn+1+bn+1=nbn.当n=1时,有a1b2+b2=b1,即$\frac{1}{3}{a}_{1}$+$\frac{1}{3}$=1,
∴a1=2.
又∵{an}是公差为3的等差数列,∴an=3n-1.
由an=3n-1知:(3n-1)bn+1+bn+1=nbn,
化简得3bn+1=bn,即$\frac{{{b_{n+1}}}}{b_n}=\frac{1}{3}$.
即数列{bn}是以1为首项,以$\frac{1}{3}$为公比的等比数列,∴${b_n}={(\frac{1}{3})^{n-1}}$.
(II)cn=an•bn=$(3n-1)•{(\frac{1}{3})^{n-1}}$,
Tn=c1+c2+c3+…+cn,
∴${T_n}=2×{(\frac{1}{3})^0}+5×{(\frac{1}{3})^1}+8×{(\frac{1}{3})^2}+…+(3n-4)×{(\frac{1}{3})^{n-2}}+(3n-1)×{(\frac{1}{3})^{n-1}}$,
$\frac{1}{3}{T_n}=2×{(\frac{1}{3})^1}+5×{(\frac{1}{3})^2}+8×{(\frac{1}{3})^3}+…+(3n-4)×{(\frac{1}{3})^{n-1}}+(3n-1)×{(\frac{1}{3})^n}$.
∴$\frac{2}{3}{T_n}=2×{(\frac{1}{3})^0}+3×{(\frac{1}{3})^1}+3×{(\frac{1}{3})^2}+…+3×{(\frac{1}{3})^{n-2}}+3×{(\frac{1}{3})^{n-1}}-(3n-1){(\frac{1}{3})^n}$,
$\frac{2}{3}{T_n}=2+3×[{(\frac{1}{3})^1}+{(\frac{1}{3})^2}+…+{(\frac{1}{3})^{n-2}}+{(\frac{1}{3})^{n-1}}]-(3n-1){(\frac{1}{3})^n}$
$\frac{2}{3}{T_n}=2+3×\frac{{\frac{1}{3}[1-{{(\frac{1}{3})}^{n-1}}]}}{{1-\frac{1}{3}}}-(3n-1){(\frac{1}{3})^n}$,
$\frac{2}{3}{T_n}=2+\frac{3}{2}-\frac{3}{2}•{(\frac{1}{3})^{n-1}}-(3n-1){(\frac{1}{3})^n}=\frac{7}{2}-(n+\frac{7}{6}){(\frac{1}{3})^{n-1}}$,
∴${T_n}=\frac{21}{4}-\frac{3}{2}(n+\frac{7}{6}){(\frac{1}{3})^{n-1}}$.
点评 本题考查了递推关系、等差数列与等比数列的通项公式及其求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,-1) | C. | (-2,-1] | D. | [-2,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a≠0或b≠0(a,b∈R),则a2+b2≠0 | B. | 若a=b≠0(a,b∈R),则a2+b2≠0 | ||
| C. | 若a≠0且b≠0(a,b∈R),则a2+b2≠0 | D. | 若a≠b≠0(a,b∈R),则a2+b2≠0 |
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:选择题
已知函数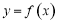 的定义域为
的定义域为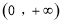 ,当
,当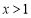 时,
时,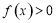 ,对任意的
,对任意的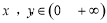 ,
,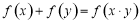 成立,若数列
成立,若数列 满足
满足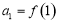 ,且
,且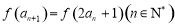 ,则
,则 的值为( )
的值为( )
A.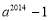 B.
B.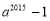 C.
C. D.
D.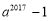
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $\frac{242}{15}$ | C. | $\frac{432}{23}$ | D. | $\frac{494}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com