
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 g(x)=$\frac{2x+sinx}{{{x^2}+1}}$,得到g(x)为奇函数,得到g(x)max+g(x)min=0,相加可得答案.
解答 解:∵f(x)=1+$\frac{2x+sinx}{{{x^2}+1}}$,
设g(x)=$\frac{2x+sinx}{{{x^2}+1}}$,
∴g(-x)=$\frac{-2x-sinx}{{x}^{2}+1}$=-$\frac{2x+sinx}{{{x^2}+1}}$=-g(x),
∴g(x)为奇函数,
∴g(x)max+g(x)min=0
∵M=1+g(x)max,N=1+g(x)min,
∴M+N=1+1+0=2,
故选:A.
点评 本题主要考查了利用函数的奇偶性求函数的最大值与最小值,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
中秋节吃月饼是我国的传统习俗,设一盘中盛有7块月饼,其中五仁月饼2块,莲蓉月饼3块,豆沙月饼2块,这三种月饼的形状大小完全相同,从中任取3块.
(Ⅰ)求这三种月饼各取到1块的概率;
(Ⅱ)设 表示取到的豆沙月饼的个数,求
表示取到的豆沙月饼的个数,求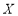 的分布列,数学期望与方差.
的分布列,数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N | B. | ∁U(M∪N) | C. | {x|x<-4或x≥2} | D. | {x|x<-3或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,-1) | C. | (-2,-1] | D. | [-2,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅⊆{x|x<4} | B. | $2\sqrt{3}∈\left\{{x|x<4}\right\}$ | C. | ∅∈{∅,{0},{1}} | D. | $\left\{{2\sqrt{3}}\right\}∈\left\{{x|x<4}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com