

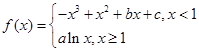 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点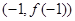 处的切线的斜率是
处的切线的斜率是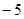 .
.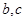 的值;
的值;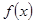 在区间
在区间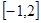 上的最大值;
上的最大值;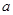 ,曲线
,曲线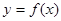 上是否存在两点
上是否存在两点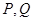 ,使得
,使得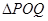 是以
是以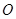 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在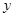 轴上?请说明理由.
轴上?请说明理由.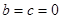 ;(2)
;(2)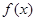 在
在 上的最大值为
上的最大值为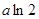 ;(3)对任意给定的正实数
;(3)对任意给定的正实数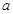 ,曲线
,曲线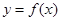 上总存在两点
上总存在两点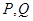 ,使得
,使得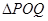 是以
是以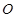 为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.
为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.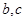 的值,由函数
的值,由函数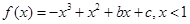 ,由图像过坐标原点
,由图像过坐标原点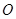 ,得
,得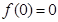 ,且根据函数在点
,且根据函数在点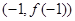 处的切线的斜率是
处的切线的斜率是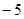 ,由导数几何意义可得
,由导数几何意义可得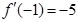 ,建立方程组,可确定实数
,建立方程组,可确定实数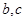 的值,进而可确定函数的解析式;(2)求
的值,进而可确定函数的解析式;(2)求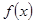 在区间
在区间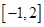 的最大值,因为
的最大值,因为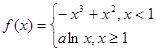 ,由于
,由于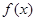 是分段函数,可分段求最大值,最后确定最大值,当
是分段函数,可分段求最大值,最后确定最大值,当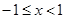 时,
时,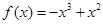 ,求导得,
,求导得,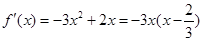 ,令
,令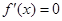 ,可得
,可得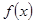 在
在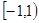 上的最大值为
上的最大值为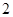 ,当
,当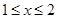 时,
时,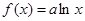 .对
.对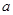 讨论,确定函数的单调性,即可求得结论;(3)这是探索性命题,可假设曲线
讨论,确定函数的单调性,即可求得结论;(3)这是探索性命题,可假设曲线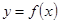 上存在两点
上存在两点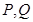 满足题设要求,则点
满足题设要求,则点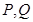 只能在
只能在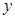 轴两侧.设
轴两侧.设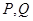 的坐标,由此入手能得到对任意给定的正实数
的坐标,由此入手能得到对任意给定的正实数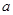 ,曲线
,曲线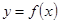 上存在两点
上存在两点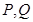 使得
使得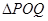 是以
是以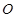 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在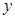 轴上.
轴上.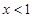 时,
时,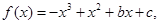 则
则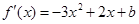 (1分)
(1分)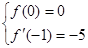 即
即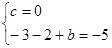 ,解得
,解得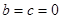 . (3分)
. (3分)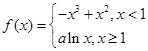
 ①当
①当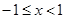 时
时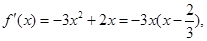 令
令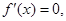 得
得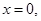 或
或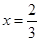 (4分)
(4分)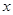 变化时
变化时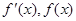 的变化情况如下表:
的变化情况如下表: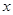 | 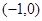 |  0 0 |  |  | (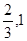 ) ) |
 | — |  0 0 |  + + |  0 0 | — |
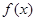 | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
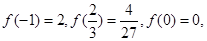
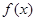 在
在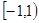 上的最大值为
上的最大值为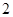 . (6分)
. (6分)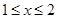 时,
时,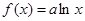
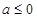 时,
时, 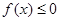 ,所以
,所以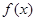 的最大值为0 ;
的最大值为0 ;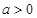 时,
时,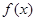 在
在 上单调递增,所以
上单调递增,所以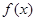 在
在 上的最大值为
上的最大值为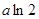 .(7分)
.(7分)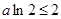 ,即
,即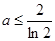 时,
时,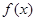 在
在 上的最大值为2;
上的最大值为2;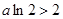 ,即
,即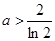 时,
时,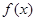 在
在 上的最大值为
上的最大值为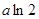 . (9分)
. (9分) 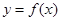 上存在两点
上存在两点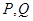 满足题设要求,则点
满足题设要求,则点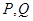 只能在y轴的两侧.
只能在y轴的两侧.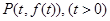 ,则
,则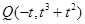 ,显然
,显然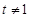
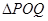 是以
是以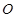 为直角顶点的直角三角形,
为直角顶点的直角三角形,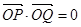 ,即
,即 ①
①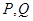 ;若方程①无解,则不存在满足题意的两点
;若方程①无解,则不存在满足题意的两点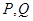
 ,则
,则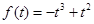 ,代入①式得
,代入①式得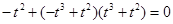 ,
,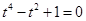 ,而此方程无实数解,因此
,而此方程无实数解,因此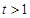 . (11分)
. (11分) 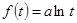 ,代入①式得,
,代入①式得, 即
即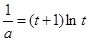 ②
②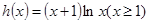 ,则
,则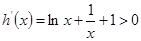 ,所以
,所以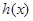 在
在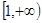 上单调递增,因为
上单调递增,因为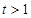 ,所以
,所以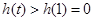 ,当
,当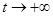 时,
时,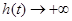 ,所以
,所以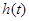 的取值范围为
的取值范围为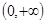 。所以对于
。所以对于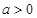 ,方程②总有解,即方程①总有解.
,方程②总有解,即方程①总有解.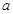 ,曲线
,曲线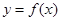 上总存在两点
上总存在两点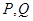 ,使得
,使得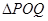 是以
是以 为直角顶点的直角三角形,且此三角形斜边的中点在y轴上. (14分)
为直角顶点的直角三角形,且此三角形斜边的中点在y轴上. (14分) 

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
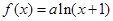 ,
,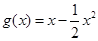 ,
,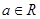
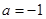 ,求曲线
,求曲线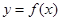 在
在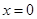 处的切线方程;
处的切线方程;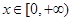 ,都有
,都有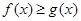 恒成立,求
恒成立,求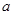 的最小值;
的最小值;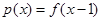 ,
,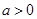 ,若
,若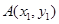 ,
,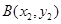 为曲线
为曲线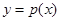 的两个不同点,满足
的两个不同点,满足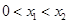 ,且
,且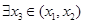 ,使得曲线
,使得曲线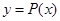 在
在 处的切线与直线AB平行,求证:
处的切线与直线AB平行,求证: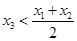
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
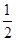 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1;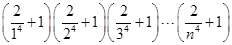 <e4(n∈N*)..
<e4(n∈N*)..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
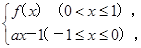 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (a为常数).
(a为常数).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
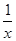 -1.
-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com