
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| | 60分以下 | 61-70分 | 71-80分 | 81-90分 | 91-100分 |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 4 | 8 | 13 | 15 | 10 |
| | 优秀人数 | 非优秀人数 | 合计 |
| 甲班 | | | |
| 乙班 | | | |
| 合计 | | | |
解:⑴由题意,甲、乙两班均有学生50人,------------------- 1分
甲班优秀人数为30人,优秀率为 ,----------- 2分
,----------- 2分
乙班优秀人数为25人,优秀率为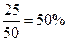 ,----------- 4分
,----------- 4分
所以甲、乙两班的优秀率分别为60%和50%.------------------- 5分
⑵
---------- 7分 优秀人数 非优秀人数 合计 甲班 30 20 50 乙班 25 25 50 合计 55 45 100
注意到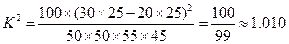 ,---------------- 11分
,---------------- 11分
所以由参考数据知,没有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助. ------------------- 12分
解析


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别
进行抽样检查,测得身高频数分布表如下表1、表2. 表1:男生身高频数分布表
表1:男生身高频数分布表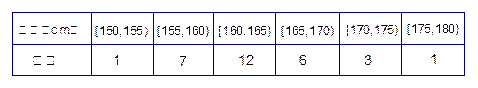 表2:女生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;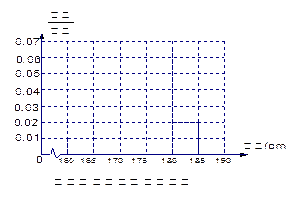
(2)估计该校学生身高(单位:cm)在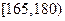 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在 的男生中任选3人,设
的男生中任选3人,设 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在 的人数,求
的人数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 假设关于某设备的使用年限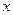 和所支出的维修费用
和所支出的维修费用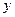 (万元)有如下的统计数据,由资料显示
(万元)有如下的统计数据,由资料显示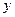 对
对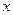 呈线性相关关系.
呈线性相关关系.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)
某种产品的广告费支出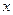 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
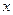 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)假设关于某市房屋面积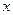 (平方米)与购房费用
(平方米)与购房费用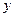 (万元),有如下的统计数据:
(万元),有如下的统计数据:
| x(平方米) | 80 | 90 | 100 | 110 |
| y(万元) | 42 | 46 | 53 | 59 |
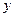 对
对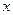 呈线性相关。
呈线性相关。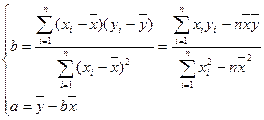
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,是总体的一样本频率分布直方图,且在[15,18)内频数为8。
(1)求样本容量;
(2)若在[12,15)内小矩形面积为0.06,求在[12,15)内的频数;
(3)求样本[18,33]内的频率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分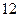 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
| | 不及格 | 及格 | 总计 |
| 甲班 | 10 | 35 | M |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | N |
 观测值的计算式
观测值的计算式 =0.6527你有多大把握认为成绩及格与班级
=0.6527你有多大把握认为成绩及格与班级 有关?
有关? =7.121又说明什么?
=7.121又说明什么?
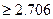 )
)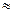 0.100,P(k
0.100,P(k
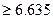 )
)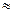 0.010)
0.010)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 | 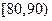 | 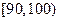 |  | 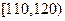 | 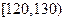 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 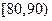 | 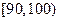 |  | 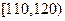 | 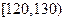 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
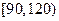 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;| | 成绩小于100分[来源:学科网ZXXK] | 成绩不小于100分 | 合计 |
| 甲班 | 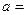 | 26 | 50 |
| 乙班 | 12 | 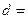 | 50 |
| 合计 | 36 | 64 | 100 |
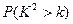 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
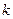 | 2.072 | 2.706 | 3.841[来源:Z.xx.k.Com] | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com