
已知函数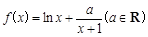 .
.
(Ⅰ)当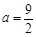 时,如果函数
时,如果函数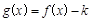 仅有一个零点,求实数
仅有一个零点,求实数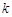 的取值范围;
的取值范围;
(Ⅱ)当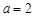 时,试比较
时,试比较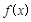 与1的大小;
与1的大小;
(Ⅲ)求证: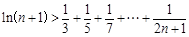
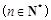 .
.
(Ⅰ)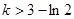 或
或
(Ⅱ)①当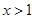 时,
时, ,即
,即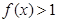 ;
;
②当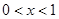 时,
时,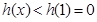 ,即
,即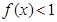 ;
;
③当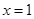 时,
时,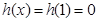 ,即
,即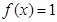 .
.
(Ⅲ)见解析
【解析】(I)当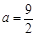 时,g(x)=f(x)-k有一个零点,实质是y=f(x)与直线y=k有一个公共点,所以利用导数研究y=f(x)的单调性,极值,最值,作出图像可求出k的取值范围.
时,g(x)=f(x)-k有一个零点,实质是y=f(x)与直线y=k有一个公共点,所以利用导数研究y=f(x)的单调性,极值,最值,作出图像可求出k的取值范围.
(II)当a=2时,令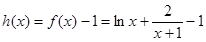 ,然后利用导数研究其单调区间及最值,然后再分类讨论f(x)与1的大小关系.
,然后利用导数研究其单调区间及最值,然后再分类讨论f(x)与1的大小关系.
(III)解本小题的关键是根据(2)的结论,当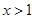 时,
时,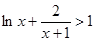 ,即
,即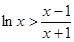 .
.
令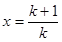 ,则有
,则有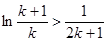 ,从而得
,从而得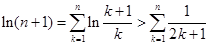 ,问题得解.
,问题得解.
解:(Ⅰ)当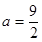 时,
时,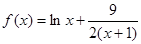 ,定义域是
,定义域是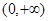 ,
,
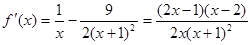 , 令
, 令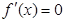 ,得
,得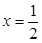 或
或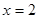 . …2分
. …2分
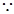 当
当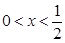 或
或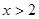 时,
时,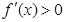 ,当
,当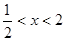 时,
时,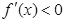 ,
,
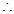 函数
函数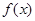 在
在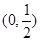 、
、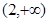 上单调递增,在
上单调递增,在 上单调递减. ……………4分
上单调递减. ……………4分
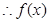 的极大值是
的极大值是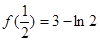 ,极小值是
,极小值是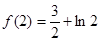 .
.
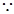 当
当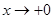 时,
时,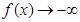 ;
;  当
当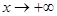 时,
时,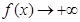 ,
,
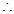 当
当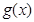 仅有一个零点时,
仅有一个零点时,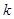 的取值范围是
的取值范围是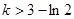 或
或 .……………5分
.……………5分
(Ⅱ)当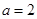 时,
时,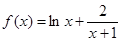 ,定义域为
,定义域为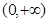 .
.
令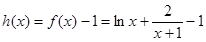 ,
,
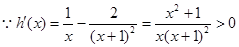 ,
, 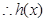 在
在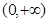 上是增函数. ………7分
上是增函数. ………7分
①当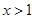 时,
时, ,即
,即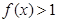 ;
;
②当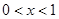 时,
时,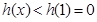 ,即
,即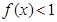 ;
;
③当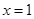 时,
时,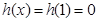 ,即
,即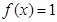 .……………9分
.……………9分
(Ⅲ)(法一)根据(2)的结论,当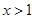 时,
时,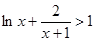 ,即
,即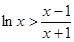 .
.
令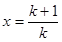 ,则有
,则有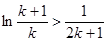 ,
,
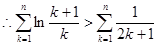 . ……………12分
. ……………12分
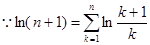 ,
,  . ……………14分
. ……………14分
(法二)当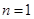 时,
时,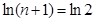 .
.
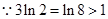 ,
,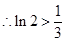 ,即
,即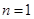 时命题成立.…………………10分
时命题成立.…………………10分
设当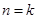 时,命题成立,即
时,命题成立,即 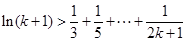 .
.
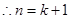 时,
时,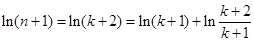
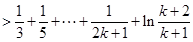 .
.
根据(Ⅱ)的结论,当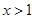 时,
时,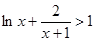 ,即
,即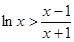 .
.
令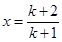 ,则有
,则有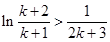 ,
,
则有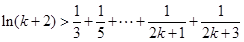 ,即
,即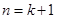 时命题也成立.……………13分
时命题也成立.……………13分
因此,由数学归纳法可知不等式成立.……………………14分
(法三)如图,根据定积分的定义,
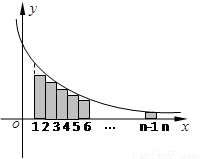
得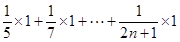
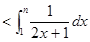 .……11分
.……11分
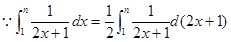
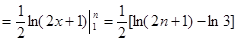 ,
,
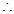
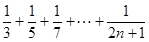
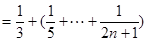

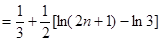 .……………………12分
.……………………12分
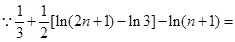
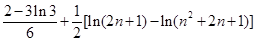 ,
,
又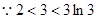 ,
,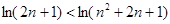 ,
,
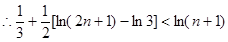 .
.
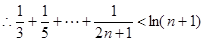 .………………14分
.………………14分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com