
分析 (1)甲、乙两人至少有一人参加,分两类:甲、乙中有一人参加,甲、乙都参加,根据分类计数原理可得,
(2)先从18人选2人和甲一组,再从先从16人选2人和乙一组,再分配到两地,根据分步计数原理可得,
(3)先求出所有的种数,再利用间接法求出队中内科医生与外科医生均不少于1名的种数,根据概率公式计算即可.
解答 解:(1)分两类:内科医生甲与某外科医生乙中有一人参加,甲、乙都参加,故有C21C185+C22C184=6936种,
(2)先从18人选2人和甲一组,再从16人选2人和乙一组,再分配到两地,共有C182C162A22=36720种,
(3)没有限制条件的种数为C206=38760种,其中全是内科医生的有C126=924种,全是外科医生有C86=28种,
则队中内科医生与外科医生均不少于1名有38760-924-28=37808种,
故队中内科医生与外科医生均不少于1名的概率为$\frac{37808}{38760}$≈0.98.
点评 本题考查排列组合知识和古典概率的知识,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 24种 | C. | 36种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
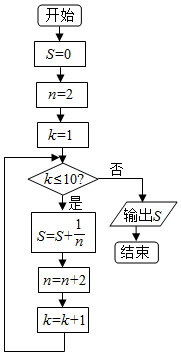
| A. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$ | ||
| C. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | D. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪{1} | B. | (-∞,1] | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com