
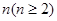 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。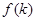 表示
表示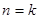 时平面被分成的区域数,则
时平面被分成的区域数,则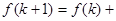 ( )
( )A. | B. | C. | D. |
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:不详 题型:解答题
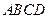 中,
中, 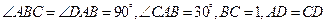 ,
,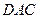 沿对角线
沿对角线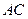 折起后如图2所示(点
折起后如图2所示(点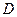 记为点
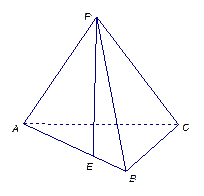
记为点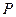 ), 点
), 点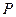 在平面
在平面 上的正投影
上的正投影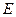 落在线段
落在线段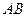 上, 连接
上, 连接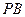 .
.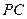 与平面
与平面 所成的角的大小;
所成的角的大小;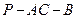 的大小的余弦值.
的大小的余弦值.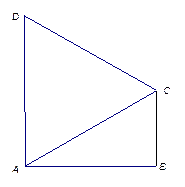
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
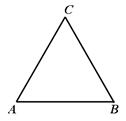
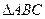 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰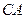 的长为
的长为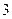 (百米),底
(百米),底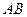 的长为
的长为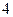 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路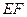 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为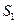 和
和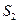 .
.
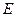 为
为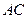 的中点,求此时小路的长度;
的中点,求此时小路的长度;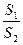 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
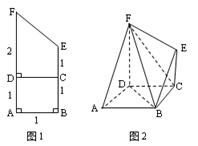
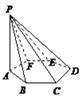
| A.∠PDA是侧面PDC与底面所成二面角的平面角 (13) | B.PC的长是点P到直线CD的距离 (14) | C.EF的长是点E到平面AFP的距离 (15) | D.∠PCB是侧棱PC与底面所成的线面角 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
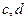 是异面直线,直线
是异面直线,直线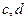 分别与
分别与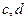 相交于两点,则
相交于两点,则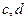 是异面直线;
是异面直线;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com