
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的必要不充分条件;③命题“
”的必要不充分条件;③命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;④命题“若
”;④命题“若![]() ,则
,则![]() ”的逆命题为真命题.其中所有正确命题的序号是_________.
”的逆命题为真命题.其中所有正确命题的序号是_________.
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】如图,某市有相交于点O的一条东西走向的公路l,与南北走向的公路m,这两条公路都与一块半径为1(单位:千米)的圆形商城A相切.根据市民建议,欲再新建一条公路PQ,点P、Q分别在公路l、m上,且要求PQ与圆形商城A也相切.
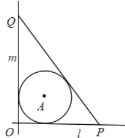
(1)当P距O处4千米时,求OQ的长;
(2)当公路PQ长最短时,求OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)试求函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式: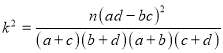
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,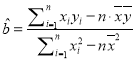 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,画出频率分布直方图(如图所示).
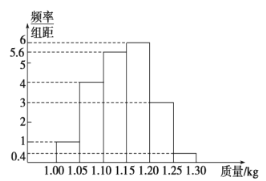
(1)在下面表格中填写相应的频率;
分组 | 频率 |
| |
| |
| |
| |
| |
|
(2)估计数据落在![]() 中的概率;
中的概率;
(3)将上面捕捞的100条鱼分别作一记分组频率号后再放回水库.几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条.请根据这一情况来估计该水库中鱼的总条数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com