
【题目】已知函数![]() .
.
(1)试求函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
【答案】(1)有唯一极小值点,没有极大值点.(2)10
【解析】
(1)对函数求导可得![]() ,先判断
,先判断![]() 在
在![]() 单调递增,结合
单调递增,结合![]() 的符号即可得结果;(2)结合(1)中的结论,
的符号即可得结果;(2)结合(1)中的结论,![]() 有唯一极小值点
有唯一极小值点![]() ,故原题等价于
,故原题等价于![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() 在
在![]() 单调递减,结合表中数据存在唯一正数
单调递减,结合表中数据存在唯一正数![]() ,使得
,使得![]() ,从而
,从而![]() ,当
,当![]() 时,易知不等式成立,当
时,易知不等式成立,当![]() 时,等价于
时,等价于![]() ,令
,令![]() ,通过导数判断出
,通过导数判断出![]() 的单调性,可得
的单调性,可得![]() ,接着证明
,接着证明![]() 时,满足题意即可.
时,满足题意即可.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,![]() 时,
时,![]() ,
,
∴存在唯一正数![]() ,使得
,使得![]() ,
,
函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴函数![]() 有唯一极小值点
有唯一极小值点![]() ,没有极大值点,
,没有极大值点,
∴当![]() 时,
时,![]() 有唯一极小值点,没有极大值点.
有唯一极小值点,没有极大值点.
(2)由(1)知,当![]() 时,
时,![]() 有唯一极小值点
有唯一极小值点![]() ,
,
∴![]() ,
,![]() 恒成立
恒成立![]()
![]() ,∴
,∴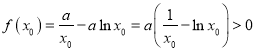 ,
,
∴![]() .
.
令![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,
由于![]() ,
,![]() ,
,
∴存在唯一正数![]() ,使得
,使得![]() ,从而
,从而![]() ,
,
由于![]() 恒成立,
恒成立,
①当![]() 时,
时,![]() 成立;
成立;
②当![]() 时,由于
时,由于![]() ,∴
,∴![]() .
.
令![]() ,当
,当![]() 时,
时,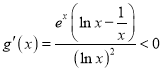 ,
,
∴![]() 在
在![]() 单调递减,从而
单调递减,从而![]() .
.
![]() ,且
,且![]() ,且
,且![]() ,
,
∴![]() .
.
下面证明![]() 时,
时,![]() .
.
![]() ,且
,且![]() 在
在![]() 单调递增,由于
单调递增,由于![]() ,
,![]() ,
,
∴存在唯一![]() ,使得
,使得![]() ,
,
∴ .
.
令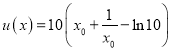 ,
,![]() ,易知
,易知![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,
,
∴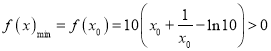 ,即
,即![]() 时,
时,![]() .
.
∴![]() 的最大值是10.
的最大值是10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在正数p,使得
,若存在正数p,使得![]() 对任意
对任意![]() 都成立,则称数列
都成立,则称数列![]() 为“拟等比数列”.
为“拟等比数列”.
![]() 已知
已知![]() ,
,![]() 且
且![]() ,若数列
,若数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() 且
且![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的取值范围;
的取值范围;
![]() 求证:数列
求证:数列![]() 是“拟等比数列”;
是“拟等比数列”;
![]() 已知等差数列
已知等差数列![]() 的首项为
的首项为![]() ,公差为d,前n项和为
,公差为d,前n项和为![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() 是“拟等比数列”,求p的取值范围
是“拟等比数列”,求p的取值范围![]() 请用
请用![]() ,d表示
,d表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在线段![]() 的两端点各置一个光源,已知光源
的两端点各置一个光源,已知光源![]() ,
,![]() 的发光强度之比为
的发光强度之比为![]() ,则线段上光照度最小的一点到
,则线段上光照度最小的一点到![]() ,
,![]() 的距离之比为______(光学定律:
的距离之比为______(光学定律:![]() 点的光照度与
点的光照度与![]() 到光源的距离的平方成反比,与光源的发光强度成正比)
到光源的距离的平方成反比,与光源的发光强度成正比)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足:
满足:![]() ,
,![]() (其中
(其中![]() 为非零实常数).
为非零实常数).
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出通项公式;
是等差数列,并求出通项公式;
(2)设![]() ,记
,记![]() ,求使得不等式
,求使得不等式![]() 成立的最小正整数
成立的最小正整数![]() ;
;
(3)若![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有![]() ,当
,当![]() 、
、![]() 、
、![]() 依次成等比数列时,求
依次成等比数列时,求![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )
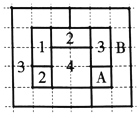
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知椭圆的焦点在![]() 轴上,其离心率为
轴上,其离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
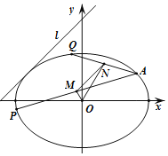
(1)求椭圆的标准方程;
(2)椭圆的弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,若
,若![]() 平行于
平行于![]() ,直线
,直线![]() 与椭圆相切,且斜率为1,则
与椭圆相切,且斜率为1,则![]() ,
,![]() 斜率之和是否为定值?若是定值,请求出该定值;若不是定值请说明理由.
斜率之和是否为定值?若是定值,请求出该定值;若不是定值请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为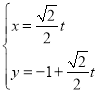 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的必要不充分条件;③命题“
”的必要不充分条件;③命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;④命题“若
”;④命题“若![]() ,则
,则![]() ”的逆命题为真命题.其中所有正确命题的序号是_________.
”的逆命题为真命题.其中所有正确命题的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com