
【题目】在线段![]() 的两端点各置一个光源,已知光源
的两端点各置一个光源,已知光源![]() ,
,![]() 的发光强度之比为
的发光强度之比为![]() ,则线段上光照度最小的一点到
,则线段上光照度最小的一点到![]() ,
,![]() 的距离之比为______(光学定律:
的距离之比为______(光学定律:![]() 点的光照度与
点的光照度与![]() 到光源的距离的平方成反比,与光源的发光强度成正比)
到光源的距离的平方成反比,与光源的发光强度成正比)
【答案】![]()
【解析】
设线段长为L,线段上光照度最小的一点P到![]() ,
,![]() 的距离分别为
的距离分别为![]() ,不妨设
,不妨设![]() ,
,![]() 光源的发光强度之比为1,2,由题意可得P点受光源
光源的发光强度之比为1,2,由题意可得P点受光源![]() 的照度为:
的照度为:![]() ,P点受光源
,P点受光源![]() 的照度为:
的照度为:![]() ,作和后利用导数求最值,可得P到
,作和后利用导数求最值,可得P到![]() ,
,![]() 的距离,作比得答案.
的距离,作比得答案.
解:设线段长为L,线段上光照度最小的一点P到![]() ,
,![]() 的距离分别为
的距离分别为![]() ,不妨设
,不妨设![]() ,
,![]() 光源的发光强度为1,2,
光源的发光强度为1,2,
∵光照度与光的强度成正比,设比例系数为![]() ,
,
与光源距离的平方成反比,设比例系数为![]() ,
,
故P点受光源![]() 的照度为:
的照度为:![]() ,
,
P点受光源![]() 的照度为:
的照度为:![]() ,
,
故P点受到![]() ,
,![]() 两光源的总照度
两光源的总照度![]() ,
,
![]()
![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上递减,
上递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上递增,
上递增,
故当![]() 时,
时,![]() 取极小值,且是最小值,
取极小值,且是最小值,
故P在线段![]()
![]() 上距离
上距离![]() 为
为![]() 时,P点的光照度最小,
时,P点的光照度最小,
此时点P到的距离![]() ,
,![]() 之比为
之比为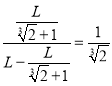 .
.
故答案为:![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分 组 | 频 数 | 频 率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 |
|
[80,90) |
|
|
[90,100] | 14 | 0.28 |
合 计 |
| 1.00 |
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级学生成绩的中位数;
(3)如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市有相交于点O的一条东西走向的公路l,与南北走向的公路m,这两条公路都与一块半径为1(单位:千米)的圆形商城A相切.根据市民建议,欲再新建一条公路PQ,点P、Q分别在公路l、m上,且要求PQ与圆形商城A也相切.
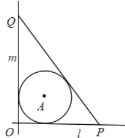
(1)当P距O处4千米时,求OQ的长;
(2)当公路PQ长最短时,求OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 作一条斜率不为
作一条斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记点
两点,记点![]() 关于
关于![]() 轴对称的点为
轴对称的点为![]() .证明:直线
.证明:直线![]() 经过
经过![]() 轴上一定点
轴上一定点![]() ,并求出定点
,并求出定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)试求函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com