
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于0的常数),现随机抽取6件合格产品,测得数据如下:
为大于0的常数),现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
(1)求![]() 关于
关于![]() 的回归方程;(提示:
的回归方程;(提示:![]() 与
与![]() 有线性相关关系)
有线性相关关系)
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
参考数据及公式:
![]() ,
,![]() ,
,![]() ,
,![]()
对于样本![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
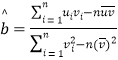 ,
,![]()
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)对![]() 两边取自然对数得
两边取自然对数得![]() ,令
,令![]() ,
,![]() ,结合线性回归方程的计算公式可得回归方程为
,结合线性回归方程的计算公式可得回归方程为![]() .
.
(2)由题意可得优等品有3件.由题意可知从6件合格品中选出3件的方法数共20种;其中恰 好有2件为优等品的取法共9种;则恰好取得两件优等品的概率为![]() .
.
详解:(1)对![]() 两边取自然对数得
两边取自然对数得![]() ,
,
令![]() ,
,![]() ,得:
,得:![]() ,
,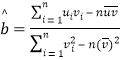
![]() ,
,![]() ,
,
解得:![]() ,所以
,所以![]() ,回归方程为
,回归方程为![]() .
.
(2)令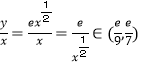 ,解得:
,解得:![]() ,∴
,∴![]() ,即优等品有3件.
,即优等品有3件.
设“恰好取得两件优等品”记为事件![]() ,记优等品为
,记优等品为![]() ,其余产品为1,2,3,
,其余产品为1,2,3,
则从6件合格品中选出3件的方法数为:![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共20种;
共20种;
其中恰 好有2件为优等品的取法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共9种;
,共9种;
所以,恰好取得两件优等品的概率为![]() .
.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】古希腊亚历山大时期的数学家帕普斯(Pappus,约300~约350)在《数学汇编》第3卷中记载着一个定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以重心旋转所得周长的积.”如图,半圆![]() 的直径
的直径![]() ,点
,点![]() 是该半圆弧的中点,半圆弧与直径
是该半圆弧的中点,半圆弧与直径![]() 所围成的半圆面(阴影部分不含边界)的重心
所围成的半圆面(阴影部分不含边界)的重心![]() 位于对称轴
位于对称轴![]() 上.若半圆面绕直径
上.若半圆面绕直径![]() 所在直线旋转一周,则所得到的旋转体的体积为__________
所在直线旋转一周,则所得到的旋转体的体积为__________![]() ,
,![]() ___________________
___________________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com