
| AЃЎ | 1 | BЃЎ | 3 | CЃЎ | 5 | DЃЎ | 10 |
ЗжЮі зіГіfЃЈxЃЉЕФКЏЪ§ЭМЯѓЃЌХаЖЯfЃЈxЃЉ=tЕФНтЕФЧщПіЃЌИљОнf2ЃЈxЃЉ+bfЃЈxЃЉ+c=0ЕФНтЕУИіЪ§ХаЖЯfЃЈxЃЉЕФЗЖЮЇЃЌЕУГіx1ЃЌx2ЃЌx3ЃЎ
НтД№ НтЃКСюfЃЈxЃЉ=tЃЌзіГіfЃЈxЃЉЕФКЏЪ§ЭМЯѓШчЯТЃК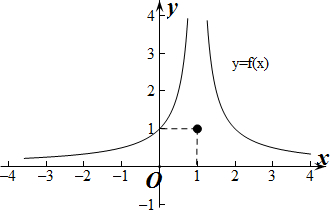
гЩЭМЯѓПЩжЊЕБt=1ЪБЃЌfЃЈxЃЉ=tгаШ§НтЃЌ
ЕБ0ЃМtЃМ1ЛђtЃО1ЪБЃЌfЃЈxЃЉ=tгаСННтЃЌ
ЕБtЁм0ЪБЃЌЗНГЬfЃЈxЃЉ=tЮоНтЃЎ
ЁпЙигкxЕФЗНГЬf2ЃЈxЃЉ+bfЃЈxЃЉ+c=0гаШ§ИіВЛЭЌЕФНтx1ЃЌx2ЃЌx3ЃЌ
ЁрfЃЈxЃЉ=1ЃЌ
ЕБxЃМ1ЪБЃЌСю$\frac{1}{1-x}$=1НтЕУx=0ЃЌ
ЕБxЃО1ЪБЃЌСю$\frac{1}{x-1}=1$НтЕУx=2ЃЌ
ЕБx=1ЪБЃЌЯдШЛx=1ЪЧfЃЈxЃЉ=1ЕФНтЃЎ
ВЛЗСЩшx1ЃМx2ЃМx3ЃЌдђx1=0ЃЌx2=1ЃЌx3=2ЃЌ
Ёр${x_1}^2+{x_2}^2+{x_3}^2$=5ЃЎ
ЙЪбЁCЃЎ
ЕуЦР БОЬтПМВщСЫКЏЪ§СуЕуЕФИіЪ§гыКЏЪ§ЭМЯѓЕФЙиЯЕЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{{\sqrt{2}}}{2}$ | BЃЎ | $\sqrt{2}$ | CЃЎ | 2$\sqrt{2}$ | DЃЎ | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | y=2x-1 | BЃЎ | y=-x+1 | CЃЎ | y=x-1 | DЃЎ | y=-2x+2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ЩшЭждВ$MЃК\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$ЃЌЦфжаcЃО0ЃЎ
ЩшЭждВ$MЃК\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$ЃЌЦфжаcЃО0ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
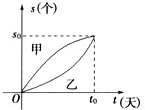 ФГЪжЛњХфМўЩњВњСїЫЎЯпЙВгаМзЁЂввСНЬѕЃЌВњСПsЃЈЕЅЮЛЃКИіЃЉгыЪБМфtЃЈЕЅЮЛЃКЬьЃЉЕФЙиЯЕШчЭМЫљЪОЃЌдђНгНќt0ЬьЪБЃЌЯТСаНсТлжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ФГЪжЛњХфМўЩњВњСїЫЎЯпЙВгаМзЁЂввСНЬѕЃЌВњСПsЃЈЕЅЮЛЃКИіЃЉгыЪБМфtЃЈЕЅЮЛЃКЬьЃЉЕФЙиЯЕШчЭМЫљЪОЃЌдђНгНќt0ЬьЪБЃЌЯТСаНсТлжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | МзЕФШеЩњВњСПДѓгкввЕФШеЩњВњСП | |
| BЃЎ | МзЕФШеЩњВњСПаЁгкввЕФШеЩњВњСП | |
| CЃЎ | МзЕФШеЩњВњСПЕШгкввЕФШеЩњВњСП | |
| DЃЎ | ЮоЗЈХаЖЈМзЕФШеЩњВњСПгыввЕФШеЩњВњСПЕФДѓаЁ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 8 | BЃЎ | 6 | CЃЎ | 4 | DЃЎ | 2 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com