
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点M,N分别是A1B和A1C的中点.
如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点M,N分别是A1B和A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0,2} | B. | {-2,2,4} | C. | {-2,0,3} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
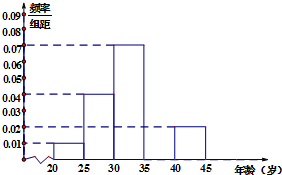 随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.
随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | 20 | 0.20 |
| [30,35) | ① | 0.350 |
| [35,40) | 30 | ② |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△ADE,使得点A'在平面EBCD上的投影在CD上,且直线A'D与平面EBCD所成角为30°,则线段AE的长为$\frac{4\sqrt{3}}{3}$.
如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△ADE,使得点A'在平面EBCD上的投影在CD上,且直线A'D与平面EBCD所成角为30°,则线段AE的长为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 5 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com