
分析 (1)由题意列方程,求得q和a2,根据等比数列和等差数列通项公式即可求得an与bn;
(2)由(1),求得Sn=$\frac{n(3+3n)}{2}$,则$\frac{1}{{S}_{n}}$=$\frac{2}{3n(n+1)}$=$\frac{2}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),采用“裂项法”即可求得$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$.
解答 解:(1)由已知条件可知:$\left\{\begin{array}{l}{q+3+{a}_{2}=12}\\{q=\frac{3+{a}_{3}}{q}}\end{array}\right.$,
解得:q=3,q=-4(舍去),
a2=6,
∴an=3+3(n-1)=3n,bn=1•3n-1,
∴an=3n,bn=3n-1,
(2)Sn=$\frac{n(3+3n)}{2}$,
∴$\frac{1}{{S}_{n}}$=$\frac{2}{3n(n+1)}$=$\frac{2}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),
$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$=$\frac{2}{3}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$).
=$\frac{2}{3}$(1-$\frac{1}{n+1}$),
=$\frac{2n}{3(n+1)}$,
∴$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$=$\frac{2n}{3(n+1)}$.
点评 本题考查等差数列和等比数列通项公式,考查“裂项法”求数列的前n项和,考查计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | -$\frac{3π}{4}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
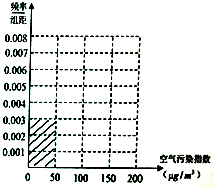 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别是为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年8月某日某省x个监测点数据统计如表:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别是为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年8月某日某省x个监测点数据统计如表:| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com