Question

13．已知点P是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）右支上一点，F₁、F₂分别为双曲线的右、右焦点，若I为△PF₁F₂的内心，则S_△IPF1-S_△IPF2=$\frac{a}{{\sqrt{{a^2}+{b^2}}}}{S_{△I{F_1}{F_2}}}$成立．请类比该结论得出有关椭圆的一个结论并进行证明．

Answer 1

分析 设△PF₁F₂的内切圆半径为r，由|PF₁|+|PF₂|=2a，|F₁F₂|=2c，|PF₁|+|PF₂|=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$•2c用△PF₁F₂的边长和r表示出三角形的面积，即可得出结论．

解答 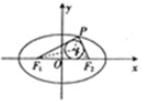解：类比该结论得出有关椭圆的一个结论：${S}_{△IP{F}_{1}}$+${S}_{△IP{F}_{2}}$=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$•${S}_{△I{F}_{1}{F}_{2}}$，设△PF₁F₂的内切圆半径为r，由双曲线的定义得|PF₁|+|PF₂|=2a，|F₁F₂|=2c，|PF₁|+|PF₂|=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$•2c
${S}_{△IP{F}_{1}}$=$\frac{1}{2}$|PF₁|•r，${S}_{△IP{F}_{2}}$=$\frac{1}{2}$|PF₂|•r，•${S}_{△I{F}_{1}{F}_{2}}$=$\frac{1}{2}$•2c•r=cr，
∴$\frac{1}{2}$|PF₁|•r+|PF₂|•r=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$••${S}_{△I{F}_{1}{F}_{2}}$，
∴${S}_{△IP{F}_{1}}$+${S}_{△IP{F}_{2}}$=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$••${S}_{△I{F}_{1}{F}_{2}}$．

点评 本题考查类比推理，考查双曲线、椭圆的定义和简单性质，利用待定系数法求出参数的值，属于基础题．