练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．一物体在力F（x）=5x+2（x单位为m，F单位为N）的作用下，沿着与力F相同的方向从x=0处运动到x=4处，则力F所作的功是（　　）
    A．40B．42C．48D．52

    分析 根据定积分的物理意义计算．

    解答 解：W=${{∫}_{0}}^{4}（5x+2）dx$=$（\frac{5}{2}{x}^{2}+2x）{{|}_{0}}^{4}$=48．
    故选：C．

    点评 本题考查了定积分的物理背景及应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．数列{an}中，若a1=1，a2=2，an+2=an+2，则数列的通项公式an=n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，若a=2，A=30°，B=45°，则边b的大小为（　　）
    A．$2\sqrt{2}$B．2C．$\sqrt{6}+\sqrt{2}$D．$\sqrt{6}+\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．某班学生在一次月考中数学不及格的占16%，语文不及格的占7%，两门都不及格的占4%，已知该班某学生在月考中语文不及格，则该学生在月考中数学不及格的概率是（　　）
    A．$\frac{1}{4}$B．$\frac{7}{16}$C．$\frac{4}{7}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，左焦点为F（-1，0），过D（0，2）且斜率为k的直线l交椭圆于A，B两点．
    （1）求椭圆C的标准方程；
    （2）在y轴上，是否存在定点E，$\overrightarrow{AE}$•$\overrightarrow{BE}$恒为定值？若存在，求出E点的坐标和这个定值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若双曲线$\frac{x^2}{9}$-$\frac{y^2}{m}$=1的离心率为$\frac{{\sqrt{14}}}{3}$，则双曲线焦点F到渐近线的距离为（　　）
    A．2B．$\sqrt{14}$C．$\sqrt{5}$D．2$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

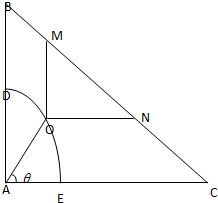    16．如图所示，某居民小区内建一块直角三角形草坪ABC，直角边AB=40米，AC=40$\sqrt{3}$米，扇形花坛ADE是草坪的一部分，其半径为20米，为了便于居民平时休闲散步，该小区物业管理公司将在这块草坪内铺设两条小路OM和ON，考虑到小区整体规划，要求M、N在斜边BC上，O在弧$\widehat{DE}$上，OM∥AB，ON∥AC，．
    （1）设∠OAE=θ，记f（θ）=OM+ON，求f（θ）的表达式，并求出此函数的定义域；
    （2）经核算，两条路每米铺设费用均为400元，如何设计θ的大小使铺路的总费用最低？并求出最低总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知点P是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）右支上一点，F1、F2分别为双曲线的右、右焦点，若I为△PF1F2的内心，则S△IPF1-S△IPF2=$\frac{a}{{\sqrt{{a^2}+{b^2}}}}{S_{△I{F_1}{F_2}}}$成立．请类比该结论得出有关椭圆的一个结论并进行证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知tanα=$\frac{1}{3}$，tanβ=-$\frac{1}{7}$，α∈（0，$\frac{π}{2}$），β∈（$\frac{π}{2}$，π），则2α-β的值是（　　）
    A．-$\frac{π}{4}$B．$\frac{π}{4}$C．-$\frac{3π}{4}$D．$\frac{3π}{4}$

    查看答案和解析>>

    同步练习册答案