
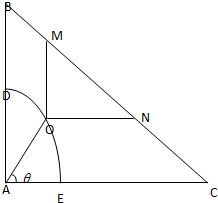
 如图所示,某居民小区内建一块直角三角形草坪ABC,直角边AB=40米,AC=40$\sqrt{3}$米,扇形花坛ADE是草坪的一部分,其半径为20米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设两条小路OM和ON,考虑到小区整体规划,要求M、N在斜边BC上,O在弧$\widehat{DE}$上,OM∥AB,ON∥AC,.
如图所示,某居民小区内建一块直角三角形草坪ABC,直角边AB=40米,AC=40$\sqrt{3}$米,扇形花坛ADE是草坪的一部分,其半径为20米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设两条小路OM和ON,考虑到小区整体规划,要求M、N在斜边BC上,O在弧$\widehat{DE}$上,OM∥AB,ON∥AC,.分析 (1)过O、N作AC的垂线交AC与F、G两点,求出OM,ON,即可求出f(θ)的表达式,并求出此函数的定义域;
(2)利用辅助角公式化简,即可得出结论.
解答 解:(1)如图过O、N作AC的垂线交AC与F、G两点,则AF=20cosθ,OF=NG=20sinθ,CG=20$\sqrt{3}sinθ$,
∴ON=$40\sqrt{3}-20(\sqrt{3}sinθ+cosθ)$,OM═$\frac{{\sqrt{3}}}{3}$ON,
则l=(1+$\frac{\sqrt{3}}{3}$)[$40\sqrt{3}-20(\sqrt{3}sinθ+cosθ)$],$θ∈[{0,\frac{π}{2}}]$,…8分
(2)$l=({1+\frac{{\sqrt{3}}}{3}})[40\sqrt{3}-40sin(θ+\frac{π}{6})]$,…12分
∵$θ∈[{0,\frac{π}{2}}]$,
∴$θ+\frac{π}{6}∈[{\frac{π}{6},\frac{2π}{3}}]$,
∴$当θ+\frac{π}{6}=\frac{π}{2}$,即$θ=\frac{π}{3}$,总费用最少为$\frac{32000}{3}\sqrt{3}$…16分.
点评 本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.


科目:高中数学 来源: 题型:解答题
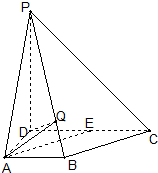 四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AD⊥DC,且AB=AD=1,PD=DC=2,E是CD的中点.
四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AD⊥DC,且AB=AD=1,PD=DC=2,E是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 6 | C. | -6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 42 | C. | 48 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 理科 | 文科 | 总计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 总计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点M,N分别是A1B和A1C的中点.
如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点M,N分别是A1B和A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0,2} | B. | {-2,2,4} | C. | {-2,0,3} | D. | {0,2,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com