
分析 通过球的内接体,说明几何体的中心是球的直径,设出三棱柱的底面边长,由棱柱的体积公式得到三棱柱的底面边长,可得球的半径,由球的表面积求出球的表面积.
解答 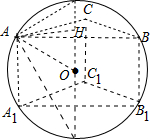 解:如图,
解:如图,
∵三棱柱ABC-A1B1C1的所有棱长都相等,6个顶点都在球O的球面上,
∴三棱柱为正三棱柱,且其中心为球的球心,设为O,
设三棱柱的底面边长为a,则
∵三棱柱的体积为$\frac{9}{4}$,∴$\frac{\sqrt{3}}{4}{a}^{2}•a$=$\frac{9}{4}$,∴a=$\sqrt{3}$.
设球的半径为r,上底面所在圆的半径为$\frac{\sqrt{3}}{3}$a=1,且球心O到上底面中心H的距离OH=$\frac{a}{2}$=$\frac{\sqrt{3}}{2}$,
∴r=$\sqrt{1+\frac{3}{4}}$=$\frac{\sqrt{7}}{2}$,
∴球O的表面积为4πr2=7π
故答案为:7π
点评 本题考查球的内接体与球的关系,球的半径的求解,考查计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
| 理科 | 文科 | 总计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 总计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0,2} | B. | {-2,2,4} | C. | {-2,0,3} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCD-EFQH材料切割成三棱锥H-ACF.
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCD-EFQH材料切割成三棱锥H-ACF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
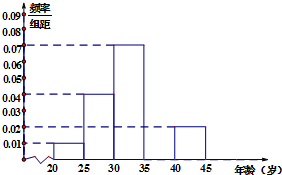 随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.
随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | 20 | 0.20 |
| [30,35) | ① | 0.350 |
| [35,40) | 30 | ② |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
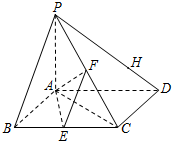 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com