
| A. | 3 | B. | 2 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
分析 先根据抛物线方程求得准线方程,代入双曲线方程求得y,根据双曲线的对称性可知△FAB为等腰直角三角形,进而可求得A或B的纵坐标为4,进而求得a,利用a,b和c的关系求得c,则双曲线的离心率可得.
解答 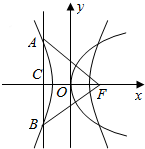 解:依题意知抛物线的准线x=-2,代入双曲线方程得
解:依题意知抛物线的准线x=-2,代入双曲线方程得
y=±$\frac{4}{a}$•$\sqrt{4{-a}^{2}}$,不妨设A(-2,$\frac{4}{a}$$\sqrt{4{-a}^{2}}$).
∵△FAB是等腰直角三角形,∴$\frac{4}{a}$$\sqrt{4{-a}^{2}}$=p=4,求得a=$\sqrt{2}$,
∴双曲线的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+16}}{a}$=$\frac{\sqrt{18}}{\sqrt{2}}$=3,
故选:A.
点评 本题主要考查了双曲线的简单性质.解题的关键是通过双曲线的对称性质判断出△FAB为等腰直角三角形,属于中档题.


科目:高中数学 来源: 题型:填空题
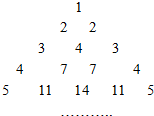 如图所示,一个左右对称的三角形数阵,其第n行共有n个数,每一行的第一个数依次组成等差数列,从第三行起每一行中除了第一个数和最后一个数外,每一个数都等于它肩上的两个数字之和,记第i行的第j个数为f(i,j),则当n≥3时,f(n,2)=$\frac{n(n-1)}{2}+1$.
如图所示,一个左右对称的三角形数阵,其第n行共有n个数,每一行的第一个数依次组成等差数列,从第三行起每一行中除了第一个数和最后一个数外,每一个数都等于它肩上的两个数字之和,记第i行的第j个数为f(i,j),则当n≥3时,f(n,2)=$\frac{n(n-1)}{2}+1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
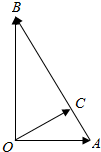 如图所示,已知∠B=30°,∠A0B=90°,点C在AB上,0C⊥AB,用$\overrightarrow{OA}和\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$.
如图所示,已知∠B=30°,∠A0B=90°,点C在AB上,0C⊥AB,用$\overrightarrow{OA}和\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | ±$\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | ±$\frac{7}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com