Question

已知抛物线x²=2py(p＞0),过焦点F的动直线l交抛物线于A、B两点,抛物线在A、B两点处的切线相交于点Q,O为坐标原点.

(1)求·的值;

(2)求点Q的纵坐标;

(3)证明||²=||·||.

Answer 1

答案：(1)解:∵F(0,),又依题意直线l不与x轴垂直,

∴设直线l的方程为y=kx+.

由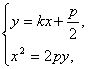可得x²-2pkx-p²=0.

设A(x₁,y₁),B(x₂,y₂),则x₁+x₂=2pk,x₁x₂=-p².

y₁y₂=(kx₁+)(kx₂+)=k²x₁x₂+(x₁+x₂)+

=-k²p²+k²p²+=,

∴·=x₁x₂+y₁y₂=p².

(2)解:由x²=2py,可得y=,∴y′=.

∴抛物线在A,B两点处的切线的斜率分别为,.

∴在点A处的切线方程为y-y₁=(x-x₁),

即y=x.

同理在点B处的切线方程为y=x.

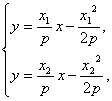解方程组可得

即点Q的纵坐标为.

(3)证明:由(2)可知,Q(pk,),

∴||²=(0-pk)²+(+)²=(1+k²)p².

又y₁+y₂=kx₁++kx₂+=k(x₁+x₂)+p=p(1+2k²),

∴||·||=(y₁+)(y₂+)=y₁y₂+(y₁+y₂)+=+(1+2k²)+=(1+k²)p².

∴||²=||·||.