
分析 (1)根据递推式计算a3,令a3=0解出λ;
(2)计算bn+1,讨论b1是否为0得出结论;
(3)求出Sn,令a<Sn<b,得出$\frac{a}{1-(-\frac{2}{3})^{n}}$<-$\frac{3}{5}$(λ+18)<$\frac{b}{1-(-\frac{2}{3})^{n}}$,从而得出-$\frac{3}{5}$(λ+18)的范围,即可得出λ的范围.
解答 解:(1)∵a1=λ,an+1=$\frac{2}{3}{a_n}$+n-4,
∴a2=$\frac{2}{3}λ$-3,a3=$\frac{2}{3}$($\frac{2}{3}$λ-3)-2=$\frac{4}{9}$λ-4,
∵a3=0,∴λ=9.
(2)∵bn=(-1)n(an-3n+21),∴bn+1=(-1)n+1(an+1-3n+18)=(-1)n+1($\frac{2}{3}$an-2n+14),
若a1-3+21=0,即λ=-18时,b1=b2=b3=…=bn=0,此时{bn}不是等比数列;
若a1-3+21≠0,即λ≠-18时,$\frac{{b}_{n+1}}{{b}_{n}}$=-$\frac{2}{3}$,此时{bn}是等比数列.
综上,当λ=-18时,{bn}不是等比数列;
当λ≠-18时,{bn}是等比数列.
(3)由(2)可知当λ=-18时,bn=0,∴Sn=0,不符合题意;
当λ≠-18时,{bn}为等比数列,公比q=-$\frac{2}{3}$,b1=-λ-18,
∴Sn=$\frac{(-λ-18)(1-(-\frac{2}{3})^{n})}{1+\frac{2}{3}}$=-$\frac{3}{5}$(λ+18)[1-(-$\frac{2}{3}$)n],
∴a<-$\frac{3}{5}$(λ+18)[1-(-$\frac{2}{3}$)n]<b,即$\frac{a}{1-(-\frac{2}{3})^{n}}$<-$\frac{3}{5}$(λ+18)<$\frac{b}{1-(-\frac{2}{3})^{n}}$,
令f(n)=1-(-$\frac{2}{3}$)n,
当n为正奇数时,1<f(n)≤$\frac{5}{3}$;当n为正偶数时$\frac{5}{9}$≤f(n)<1,
∴f(n)的最大值为f(1)=$\frac{5}{3}$,f(n)的最小值为f(2)=$\frac{5}{9}$,
∴$\frac{9}{5}$a<f(n)<$\frac{3}{5}$b,解得-18-b<λ<-3a-18.
若-b-18≥-3a-18,即b≤3a时,不存在实数λ满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18).
综上,当b>3a时,存在实数λ,使得对任意正整数n,都有a<Sn<b,λ的取值范围是(-b-18,-3a-18).
点评 本题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力,属于难题.


科目:高中数学 来源: 题型:解答题
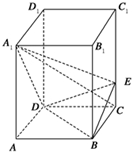 (理) 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
(理) 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sinx | B. | y=|cosx| | C. | y=sin(2x-$\frac{π}{2}$) | D. | y=tan2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?β,n?β,m∥α,n∥α,则α∥β | B. | 若m?α,m?β,α∥β,则m∥n | ||
| C. | 若α⊥β,m?α,n?β,则m⊥n | D. | 若m⊥α,n?α,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com