
分析 (1)利用an=sn-sn-1和Sn=$\frac{a}{1-a}$(1-an)整理得$\frac{{a}_{n}}{{a}_{n-1}}$=a,所以:{an}为等比数列;
(2)根据(1)an=an化简得bn.如果存在满足条件的正整数m,则m一定是偶数.b2k+2-b2k=2a2k(a2-1)(k-$\frac{{a}^{2}}{1-{a}^{2}}$)lg|a|,其中k∈N+,判断b2k+2-b2k的符号来求出m即可.
解答 解:(1)证明:当n≥2时,an=Sn-Sn-1=$\frac{a}{1-a}$(1-an-1),
整理得:$\frac{{a}_{n}}{{a}_{n-1}}$=a,
所以{an}是公比为a的等比数列;
(2)∵a1=a,∴an=an(n∈N*),
∴bn=anlg|an|=anlg|an|=nanlg|a|(n∈N*),
∵-1<a<1,
∴当n为偶数时,bn=nanlg|a|>0;当n为奇数时,bn=nanlg|a|<0,
如果存在满足条件的正整数m,则m一定是偶数,
又b2k+2-b2k=2a2k(a2-1)(k-$\frac{{a}^{2}}{1-{a}^{2}}$)lg|a|,其中k∈N*,
当a=-$\frac{\sqrt{7}}{3}$时,a2-1=$\frac{2}{9}$,
∴2a2k(a2-1)lg|a|>0,又$\frac{{a}^{2}}{1-{a}^{2}}$=$\frac{7}{2}$,
∴当k>$\frac{7}{2}$时,b2k+2>b2k,即bg<b10<b12;
当k<$\frac{7}{2}$时,b2k+2<b2k,即b8<b6<b4<b2,
故存在正整数m=8,使得对于任意正整数n都有bn≥bm.
点评 考查学生会确定等比数列的能力,运用数列求和的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
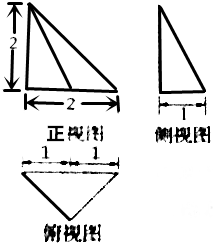
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com