
【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时.
【答案】
(1)解:设事件A为“x2+2ax+b2≥0恒成立”.
x2+2ax+b2≥0恒成立的充要条件为4a2﹣4b2≤0,即a2≤b2
基本事件共9个:(﹣1,﹣1),(﹣1,0),(﹣1,1),(0,﹣1),(0,0),(0,1),(1,﹣1),(1,0),(1,1).其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含7个基本事件:(﹣1,﹣1),(﹣1,1),(0,﹣1),(0,0),(0,1),(1,﹣1),((1,1).
事件A发生的概率为P(A)= ![]()
(2)解:设事件A为“x2+2ax+b2≥0恒成立”.
x2+2ax+b2≥0恒成立的充要条件为4a2﹣4b2≤0,即a2≤b2
试验的全部结果所构成的区域为{(a,b)|﹣1≤a≤1,﹣1≤b≤1}.
构成事件A的区域为{(a,b)|﹣1≤a≤1,﹣1≤b≤1,a2≤b2}.
如图,
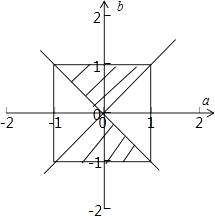
∴当a,b均为实数时,不等式x2+2ax+b2≥0恒成立的概率为 ![]()
【解析】(1)x2+2ax+b2≥0恒成立的充要条件为4a2﹣4b2≤0,即a2≤b2 , 用列举法求出基本事件数,然后直接利用古典概型概率计算公式求解;(2)由题意求出点(a,b)所构成的正方形的面积,再由线性规划知识求出满足a2≤b2的区域面积,由测度比是面积比求概率.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB∥DC,∠ABC=45°,DC=1,AB=2,PA=1.
(Ⅰ)求PD与BC所成角的大小;
(Ⅱ)求证:BC⊥平面PAC;
(Ⅲ)求二面角A﹣PC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为2的正方体ABCD﹣A1B1C1D1中,E是BC的中点,F是DD1的中点,
(1)求点A到平面A1DE的距离;
(2)求证:CF∥平面A1DE;
(3)求二面角E﹣A1D﹣A的平面角大小的余弦值.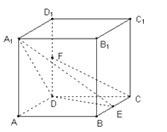
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求角B的大小;
(2)若BD为AC边上的中线,cosA= ![]() ,BD=
,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log ![]() (﹣x+1).
(﹣x+1).
(1)求f(x)的解析式;
(2)若f(a﹣1)<﹣1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com