
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (0,1) | D. | (-∞,0)∪(1,+∞) |
分析 把原函数整理成关于a的一次函数,利用一次函数的单调性求得函数在[-1,1]上的最大值,令最大值小于0,可得x的范围.
解答 解:函数可整理为f(x)=(x2-x+1)a+1-x
∵对于a∈[-1,1]时恒有f(x)<0,
∴(x2-x+1)a+1-x<0恒成立.
令g(a)=(x2-2x+1)a+1-x
则函数g(a)在区间[-1,1]上的最大值小于0,
∵g(a)为一次函数,且一次项系数x2-2x+1>0,
∴函数g(a)在区间[-1,1]上单调递增,
∴g(a)max=g(1)=x2-2x+1+1-x=x2-3x+2<0
解得1<x<2
故选:A
点评 本题主要考查了利用函数的单调性求函数最大值.在把恒成立问题转化为求函数的最值问题的过程中,体现了转化的思想.


科目:高中数学 来源: 题型:选择题
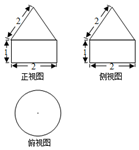
| A. | $π+\sqrt{3}π$ | B. | $\frac{4}{3}π$ | C. | $2π+\frac{{2\sqrt{3}}}{3}π$ | D. | $π+\frac{{\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a≥b,则a2≥b2”的逆否命题为“若a2≤b2,则a≤b” | |
| B. | “x=1”是“x2-3x+2=0”的必要不充分条件 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | 对于命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,x02+x0+1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{3}}}{6},\frac{{\sqrt{3}}}{6}})$ | C. | $({-\frac{{2\sqrt{2}}}{3},\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com