
已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象并判断其零点个数;
(3)根据图象指出f(x)的单调递减区间;
(4)根据图象写出不等式f(x)>0的解集;
(5)求集合M={m|使方程f(x)=m有三个不相等的实根}.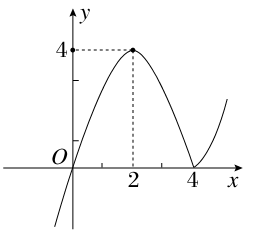
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
已知函数  的定义域是
的定义域是  ,
,  是
是  的导函数,且
的导函数,且  在
在 上恒成立
上恒成立
(Ⅰ)求函数 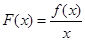 的单调区间。
的单调区间。
(Ⅱ)若函数 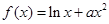 ,求实数a的取值范围
,求实数a的取值范围
(Ⅲ)设 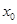 是
是  的零点 ,
的零点 , 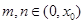 ,求证:
,求证: 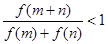 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义域为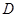 的函数
的函数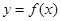 ,若同时满足:
,若同时满足:
① 在
在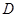 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间[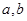 ]
]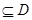 ,使
,使 在
在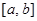 上的值域为
上的值域为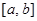 ;
;
那么把函数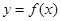 (
(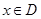 )叫做闭函数.
)叫做闭函数.
(1) 求闭函数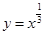 符合条件②的区间
符合条件②的区间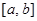 ;
;
(2) 若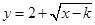 是闭函数,求实数
是闭函数,求实数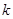 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+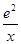 (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在区间(0,+∞)上的函数f(x)满足f(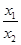 )=f(x1)-f(x2),且当x>1时,f(x)<0.
)=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).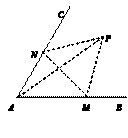
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com