
已知F1,F2分别为椭圆C1: =1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
=1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|= .
.

(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足 ,求实数λ的取值范围.
,求实数λ的取值范围.
(1)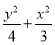 =1(2)(-2,0)∪(0,2)
=1(2)(-2,0)∪(0,2)
【解析】(1)由C2:x2=4y知F1(0,1),c=1,
设M(x0,y0)(x0<0),
因M在抛物线C2上,
故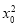 =4y0,①
=4y0,①
又|MF1|=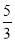 ,则y0+1=
,则y0+1=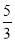 ②
②
由①②解得x0=-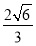 ,y0=
,y0=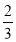 .
.
而点M在椭圆上,
∴2a=|MF1|+|MF2|=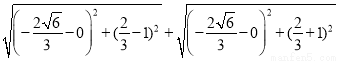 =4.
=4.
∴a=2,∴b2=a2-c2=3.
故椭圆C1的方程为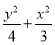 =1.
=1.
(2)因为直线l:y=k(x+t)与圆x2+(y+1)2=1相切,
所以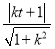 =1⇒k=
=1⇒k= (t≠0,k≠0).
(t≠0,k≠0).
把y=k(x+t)代入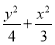 =1并整理,得
=1并整理,得
(4+3k2)x2+6k2tx+3k2t2-12=0,
设A(x1,y1),B(x2,y2),则有
x1+x2=-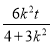 ,y1+y2=kx1+kt+kx2+kt=k(x1+x2)+2kt=
,y1+y2=kx1+kt+kx2+kt=k(x1+x2)+2kt=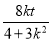 ,因为,λ
,因为,λ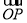 =(x1+x2,y1+y2)
=(x1+x2,y1+y2)
所以,P
又因为点P在椭圆上,
所以, +
+ =1⇒λ2=
=1⇒λ2=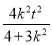 =
= (t≠0)
(t≠0)
因为t2>0,所以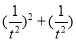 +1>1,
+1>1,
所以0<λ2<4,
当k=0时,因为直线l与圆x2+(y+1)2=1相切,
则t=0(舍去)或t=-1,
当t=-1时,
y=-1与椭圆有一个交点,不满足题意,
舍去.所以λ的取值范围是(-2,0)∪(0,2).


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x4练习卷(解析版) 题型:填空题
若直线y=kx+1被圆C:x2+y2-2x-3=0截得的弦最短,则k=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
设函数f(x)的零点为x1,函数g(x)=4x+2x-2的零点为x2,若|x1-x2|> ,则f(x)可以是( ).
,则f(x)可以是( ).
A.f(x)=2x- B.f(x)=-x2+x-
B.f(x)=-x2+x-
C.f(x)=1-10x D.f(x)=ln (8x-2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
阅读如图的程序框图,若运行相应的程序,则输出的S的值是( ).

A.102 B.39 C.81 D.21
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d4练习卷(解析版) 题型:解答题
已知函数f(x)=sin  +2cos2x-1(x∈R).
+2cos2x-1(x∈R).
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点 ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ·
·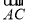 =9,求a的值.
=9,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-2练习卷(解析版) 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:选择题
设F1,F2分别是双曲线 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使( +
+ )·
)· =0,O为坐标原点,且
=0,O为坐标原点,且 =
= |
| |,则双曲线的离心率为( ).
|,则双曲线的离心率为( ).
A.  +1 B.
+1 B. 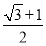 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-7练习卷(解析版) 题型:填空题
已知x>0,y>0,lg 2x+lg 8y=lg 2,则 的最小值为________.
的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com