
【题目】已知函数f(x)是定义在R上的奇函数,f(x+2)=f(x),当x∈(0,1]时,f(x)=1﹣2|x﹣ ![]() |,则函数g(x)=f[f(x)]﹣
|,则函数g(x)=f[f(x)]﹣ ![]() x在区间[﹣2,2]内不同的零点个数是( )
x在区间[﹣2,2]内不同的零点个数是( )
A.5
B.6
C.7
D.9
【答案】A
【解析】解:函数f(x)是定义在R上的奇函数,
且f(x+2)=f(x),
即有函数f(x)关于原点对称,周期为2,
当x∈(0,1]时,f(x)=1﹣2|x﹣ ![]() |,
|,
即有当x∈[﹣1,0)时,f(x)=﹣1+2|x+ ![]() |,
|,
由图象的平移可得在区间[﹣2,2]内的函数f(x)的图象,
进而得到y=f(f(x))的图象,
作出y= ![]() x的图象,由图象观察,可得它们有5个交点,
x的图象,由图象观察,可得它们有5个交点,
故零点个数为5.
故选:A.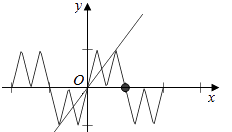
由题意可得函数f(x)的图象关于原点对称,为周期为2的函数,求得一个周期的解析式和图象,由图象平移可得[﹣2,2]的图象,得到y=f(f(x))的图象,作出y= ![]() x的图象,由图象观察即可得到零点个数.
x的图象,由图象观察即可得到零点个数.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点O,![]() 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为![]() ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为![]() ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0). (Ⅰ)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx﹣a+2
(1)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,b的值;
(2)若b=2,a>0,解关于x的不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: 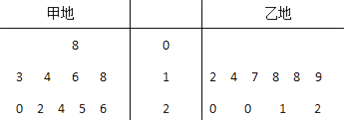
规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ﹣2lnx,a∈R.
﹣2lnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , ①求a的取值范围;
②证明:f(x2)<x2﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,D、F分别是BC、AC的中点, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
(2)求证:B、E、F三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在(﹣∞,0)∪(0,+∞)上有定义,在(0,+∞)上是增函数,f(1)=0,又知函数g(θ)=sin2θ+mcosθ﹣2m, ![]() ,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在a,b,c使等式( ![]() )2+(
)2+( ![]() )2+(
)2+( ![]() )2+…+(
)2+…+( ![]() )2=
)2= ![]() 对一切n∈N*都成立若不存在,说明理由;若存在,用数学归纳法证明你的结论.
对一切n∈N*都成立若不存在,说明理由;若存在,用数学归纳法证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com