练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    有四位学生参加三项不同的竞赛，

    ①每位学生必须参加一项竞赛，则有不同的参赛方法有           ；

    ②每项竞赛只许有一位学生参加，则有不同的参赛方法有            ；

    ③每位学生最多参加一项竞赛，每项竞赛只许有一位学生参加，则不同的参赛方法有            。


    ①学生可以选择项目，而竞赛项目对学生无条件限制，所以类似（1）可得N=34=81（种）；

    ②竞赛项目可以挑学生，而学生无选择项目的机会，每一项可以挑4种不同学生，共有N=43=64（种）；

    ③等价于从4个学生中挑选3个学生去参加三个项目的竞赛，每人参加一项，故共有C43·A33=24（种）。


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)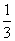＝ax3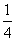－x2＋cx＋d(a，c，d∈R)满足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．

    (1)求a，c，d的值；

    (2)若h(x)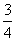＝x2－bx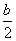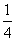＋－，解不等式f′(x)＋h(x)<0；

    (3)是否存在实数m，使函数g(x)＝f′(x)－mx在区间[m，m＋2]上有最小值－5？若存在，求出实数m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，点P(a，b)(a>b>0)为动点，F1，F2分别为椭圆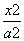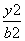＋＝1的左、右焦点，已知△F1PF2为等腰三角形．

    (1)求椭圆的离心率e；

    (2)设直线PF2与椭圆相交于A，B两点，M是直线PF2上的点，满足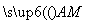·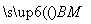＝－2，求点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(n)=3n-C1n3n-1+C2n·3n-2-…+(-1)n+log2n(n∈N*),当n=________时,|f(n)-2005|取得最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将一个四棱锥的每个顶点染上颜色，使同一条棱上的两端点异色，如果有5种颜色或供使用，那么不同的染色方法总数有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    电视台连续播放6个广告，其中含4个不同的商业广告和2个不同的公益广告，要求首尾必须播放公益广告，则共有          种不同的播放方式（结果用数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数的值是    （   ）

    A．-16           B．16

    C．-           D．8-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在复平面内，复数对应的点位于

    （A）第一象限      （B）第二象限      （C）第三象限     （D）第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y=|sinx|cosx-1的最小正周期与最大值的和为       。

    查看答案和解析>>

    同步练习册答案