练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)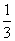＝ax3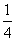－x2＋cx＋d(a，c，d∈R)满足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．

    (1)求a，c，d的值；

    (2)若h(x)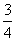＝x2－bx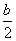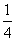＋－，解不等式f′(x)＋h(x)<0；

    (3)是否存在实数m，使函数g(x)＝f′(x)－mx在区间[m，m＋2]上有最小值－5？若存在，求出实数m的值；若不存在，请说明理由．


    ∵f′(x)≥0在R上恒成立，即ax2－x＋c≥0恒成立，

     

     

    ∵>－1，∴m＝舍去，故m＝－3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如果平面外一条直线上有两点到这个平面的距离相等，则这条直线和这个平面的位置关系是

    A．平行              B．相交                    C．平行或相交        D．不可能垂直

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知A(-2，0)，B(2，0)，点C、D满足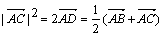

    (1)求D的轨迹；

     (2)过点A作直线l交以A、B为焦点的椭圆于M、N 两点，线段MN的中点到了轴的距离为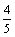，且l与D的轨迹相切，求椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数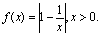

    (Ⅰ)证明:当0<a<b,且f(a)=f(b)时,ab>1;

    (Ⅱ)点P(xo,yo)(0<xo<1)在曲线y=f(x)上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用xo表示).

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知b>0，直线(b2＋1)x＋ay＋2＝0与直线x－b2y－1＝0互相垂直，则ab的最小值等于(　　)．

    A．1           B．2          C．2        D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设直线l与椭圆=1相交于A、B两点，l又与双曲线x2-y2=1相交于C、D两点，C、D三等分线段AB，求直线l的方程

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给定抛物线C：y2=4x，F是C的焦点，过点F的直线l与C相交于A、B两点

    (1)设l的斜率为1，求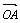与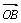夹角的大小；

    (Ⅱ)设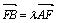，若λ∈[4，9]，求l在y轴上截距的变化范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F为抛物线y2＝2px(p>0)的焦点，A，B，C为该抛物线上三点，当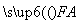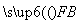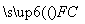＋＋＝0，且|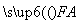|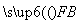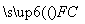＋||＋||＝3时，此抛物线的方程为(　　)

    A．y2＝2x  B．y2＝4x

    C．y2＝6x  D．y2＝8x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有四位学生参加三项不同的竞赛，

    ①每位学生必须参加一项竞赛，则有不同的参赛方法有           ；

    ②每项竞赛只许有一位学生参加，则有不同的参赛方法有            ；

    ③每位学生最多参加一项竞赛，每项竞赛只许有一位学生参加，则不同的参赛方法有            。

    查看答案和解析>>

    同步练习册答案