
用反证法证明命题“若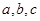 都是正数,则
都是正数,则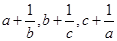 三数中至少有一个不小于
三数中至少有一个不小于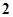 ”,提出的假设是( )
”,提出的假设是( )
A.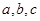 不全是正数 不全是正数 |
B.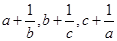 至少有一个小于 至少有一个小于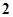 |
C.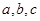 都是负数 都是负数 |
D.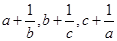 都小于2 都小于2 |
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设 ,正确顺序的序号为
,正确顺序的序号为
| A.①②③ | B.③①② | C.①③② | D.②③① |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列三句话按三段论的模式排列顺序正确的是( )
① 2013不能被2整除; ② 一切奇数都不能被2整除; ③ 2013是奇数;
| A.①②③ | B.②①③ | C.②③① | D.③②① |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
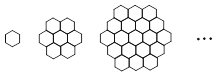
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂
巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,
以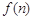 表示第
表示第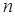 幅图的蜂巢总数,则
幅图的蜂巢总数,则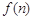 =_______.
=_______.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
请阅读下列材料:若两个正实数a1,a2满足a12+a22=1,那么a1+a2≤ .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤ .
.
根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com