已知函数f(x)=log2(ax2+2x-3a),
(1)当a=-1时,求该函数的定义域和值域;
(2)当a≤0时,如果f(x)≥1在x∈[2,3]上恒成立,求实数a的取值范围.
解:(1)当a=-1时,f(x)=log
2(ax
2+2x-3a).
令-x
2+2x+3>0,解得-1<<x<3
所以函数f(x)的定义域为(-1,3).
令t=-x
2+2x+3=-(x-1)
2+4,则0<t≤4
所以f(x)=log
2t≤log
24=2
因此函数f(x)的值域为(-∞,2]
(2)f(x)≥1在区间[2,3]上恒成立等价于ax
2+2x-3a-2≥0在区间[2,3]上恒成立
由ax
2+2x-3a-2≥0且x∈[2,3]时,x
2-3>0,得
a≥
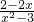
令h(x)=
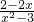
,则h′(x)=
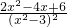
>0
所以h(x)在区间[2,3]上是增函数,所以h(x)
max=h(3)=-

因此a的取值范围是[-

,+∞).
分析:(1)当a=-1时,f(x)=log
2(ax
2+2x-3a),令-x
2+2x+3>0,解得-1<<x<3,可得函数f(x)的定义域,确定真数的范围,可得函数f(x)的值域;
(2)f(x)≥1在区间[2,3]上恒成立等价于ax
2+2x-3a-2≥0在区间[2,3]上恒成立,分离参数,构造函数,确定函数的最值,即可得到a的取值范围.
点评:本题考查函数的定义域与值域,考查恒成立问题,解题的关键是分离参数,确定函数的最值,属于中档题.

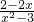
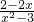 ,则h′(x)=
,则h′(x)=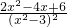 >0
>0
 ,+∞).
,+∞).
