
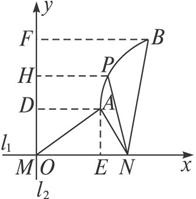
图1-5
思路分析:题中给出了相互垂直的直线l1、l2,则以l1、l2为x轴、y轴,M为坐标原点,建立坐标系的思路非常自然,设P(x,y)是曲线段C上任意一点,作PH⊥l2,H是垂足,则由题意知点P满足等式|PN|=|PH|,为求得方程,只需求得N点的坐标.

解法一:如图,建立坐标系,分别以l1、l2为x轴、y轴,M为坐标原点,作AE⊥l1,AD⊥l2,
BF⊥l2,垂足分别是E、D、F,设A(xA,yA),B(xB,yB),N(xN,0),
依题意,有xA=|ME|=|DA|=|AN|=3,yA=|DM|=![]() =
=![]() .
.
由于△AMN是锐角三角形,故有
xN=|ME|+|EN|=|ME|+![]() =4,xB=|BF|=|BN|=6.
=4,xB=|BF|=|BN|=6.
设点P(x,y)是曲线段C上任一点,作PH⊥l2,H是垂足,则由题意知P属于集合
{(x,y)|(x-xN)2+y2=x2,xA≤x≤xB,y>0}.
故曲线段C的方程为y2=8(x-2)(3≤x≤6,y>0).
解法二:如图,以l1为x轴,MN的垂直平分线为y轴建立坐标系,根据题意,曲线段C是以N为焦点,l2为准线的抛物线的一段.
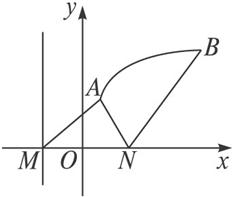
其中A、B分别为曲线C的端点.设曲线C的方程为y2=2px(p>0)(xA≤x≤xB,y>0),其中xA、xB分别为A、B的横坐标,p=|MN|.
∴M(![]() ,0),N(
,0),N(![]() ,0).
,0).
由|AM|=![]() ,|AN|=3,得
,|AN|=3,得
(xA+![]() )2+2pxA=
)2+2pxA=![]() ,①
,①
(xA-![]() )2+2pxA=9.②
)2+2pxA=9.②
联立①②,解得xA=![]() .代入①式,并由p>0,解得p=4,xA=1或p=2,xA=2.
.代入①式,并由p>0,解得p=4,xA=1或p=2,xA=2.
∵△AMN是锐角三角形,∴![]() >xA.故舍去p=2,xA=2.
>xA.故舍去p=2,xA=2.
由点B在曲线段C上,得xB=|BN|-![]() =4.
=4.
综上,得曲线段C的方程为y2=8x(1≤x≤4,y>0).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
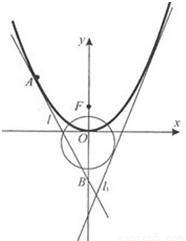
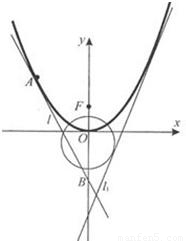
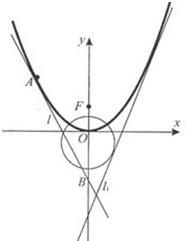 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.
如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:
图1-2-6
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省德州市乐陵一中高三(上)期末数学复习训练试卷9(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年浙江省嘉兴一中高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com