
【题目】已知函数![]() .
.
(1)将函数![]() 化成
化成![]() 的形式,并求函数
的形式,并求函数![]() 的增区间;
的增区间;
(2)若函数![]() 满足:对任意
满足:对任意![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) f(x)=![]() sin(2x+
sin(2x+![]() ) ,增区间为[-
) ,增区间为[-![]() +kπ,
+kπ, ![]() +kπ](k∈Z); (2) m≤2
+kπ](k∈Z); (2) m≤2![]()
【解析】试题分析:(1)由二倍角及两角和与差的正弦公式即可得:f(x)=![]() sin(2x+
sin(2x+![]() ),再令-
),再令-![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ,即可得到函数
+2kπ,即可得到函数![]() 的增区间;
的增区间;
(2)要使得对任意x∈[0, ![]() ]都有f(x)+m≤3
]都有f(x)+m≤3![]() 成立,即f(x)+m最大值
成立,即f(x)+m最大值![]() +m≤3
+m≤3![]() ,得m≤2
,得m≤2![]() .
.
试题解析:
(1)函数f(x)=cos(![]() -2x)+sin2x=cos
-2x)+sin2x=cos![]() cos2x +sin
cos2x +sin![]() sin2x+ sin2x
sin2x+ sin2x
=![]() sin2x+
sin2x+![]() cos2x=
cos2x=![]() (sin2x·
(sin2x·![]() +cos2x ·
+cos2x ·![]() )=
)=![]() (sin2xcos
(sin2xcos![]() +cos2xsin
+cos2xsin![]() )=
)=![]() sin(2x+
sin(2x+![]() ),
),
-![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ, 得:-
+2kπ, 得:-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,得增区间为[-
+kπ,得增区间为[-![]() +kπ,
+kπ, ![]() +kπ](k∈Z);
+kπ](k∈Z);
(2) 当x∈[0, ![]() ]时,得
]时,得![]() ≤2x+
≤2x+![]() ≤
≤![]() ,-
,-![]() ≤sin(2x+
≤sin(2x+![]() )≤1,-
)≤1,-![]() ≤
≤![]() sin(2x+
sin(2x+![]() )≤
)≤![]() ,
,
要使得对任意x∈[0, ![]() ]都有f(x)+m≤3
]都有f(x)+m≤3![]() 成立,即f(x)+m最大值
成立,即f(x)+m最大值![]() +m≤3
+m≤3![]() ,得m≤2
,得m≤2![]() .
.


科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间![]() (单位:天)的函数,且销售量满足
(单位:天)的函数,且销售量满足![]() =
=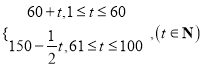 ,价格满足
,价格满足![]() =
=![]() .
.
(1)求该种商品的日销售额![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的体积为![]() ,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.

(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x).当x∈[0,1]时,f(x)=2x.若在区间[﹣2,3]上方程ax+2a﹣f(x)=0恰有四个不相等的实数根,则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2)
,2)
D.(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0 , 2 ![]() )(x0>
)(x0> ![]() )是抛物线C上一点,圆M与线段MF相交于点A,且被直线x=
)是抛物线C上一点,圆M与线段MF相交于点A,且被直线x= ![]() 截得的弦长为
截得的弦长为 ![]() |MA|,若
|MA|,若 ![]() =2,则|AF|等于( )
=2,则|AF|等于( )
A.![]()
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com