
设函数 .
.
(1)当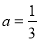 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)在(1)的条件下,设函数 ,若对于
,若对于 ,
,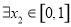 ,使
,使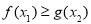 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)函数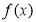 的单调递增区间为
的单调递增区间为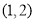 ;单调递减区间为
;单调递减区间为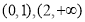
(2)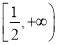
【解析】
试题分析:(1)若可导函数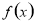 在指定的区间
在指定的区间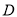 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为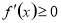
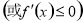 恒成立,从而构建不等式,要注意“=”是否可以取到.(2)对于恒成立的问题,常用到以下两个结论:(1)
恒成立,从而构建不等式,要注意“=”是否可以取到.(2)对于恒成立的问题,常用到以下两个结论:(1)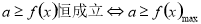 ,(2)
,(2)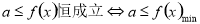
试题解析:函数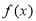 的定义域为
的定义域为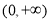 ,
,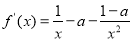
(1)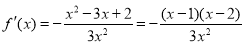
所以当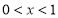 ,或
,或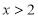 时,
时,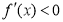 ,当
,当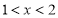 时,
时,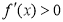 故当
故当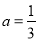 时,函数
时,函数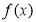 的单调递增区间为
的单调递增区间为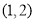 ;单调递减区间为
;单调递减区间为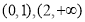
(2)当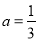 时,由(1)知函数
时,由(1)知函数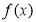 在区间
在区间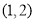 上为增函数,所以函数
上为增函数,所以函数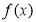 在
在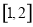 上的最小值为
上的最小值为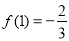
若对于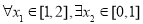 使
使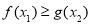 成立
成立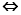
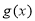 在
在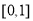 上的最小值不大于
上的最小值不大于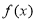 在[1,2]上的最小值
在[1,2]上的最小值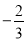 又
又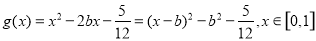
①当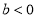 时,
时,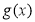 在上
在上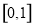 为增函数,
为增函数,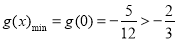 与(*)矛盾②当
与(*)矛盾②当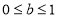 时,
时,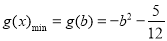 ,由
,由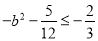 及
及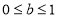 得,
得,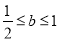 ③当
③当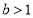 时,
时,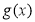 在上
在上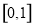 为减函数,
为减函数,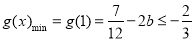 , 此时
, 此时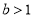 综上所述,
综上所述,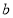 的取值范围是
的取值范围是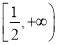
考点:函数的导数与单调性及恒成立问题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:选择题
要从已编号(1~60)的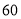 枚最新研制的某型导弹中随机抽取
枚最新研制的某型导弹中随机抽取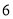 枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的
枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的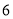 枚导弹的编号可能是( )
枚导弹的编号可能是( )
A.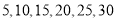 B.
B.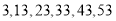
C.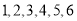 D.
D.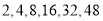
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一次检查文科数学试卷(解析版) 题型:选择题
设 是公比为q的等比数列,其前n项积为
是公比为q的等比数列,其前n项积为 ,并满足条件
,并满足条件 ,给出下列结论:①
,给出下列结论:① ②
② ③
③ ④使
④使 成立的最小自然数n等于199,则其中正确的是( )
成立的最小自然数n等于199,则其中正确的是( )
A.①②③ B.①③④ C.②③ D①②③④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一次检查文科数学试卷(解析版) 题型:选择题
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若 ,S=
,S=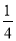 (b2+c2-a2),则∠B=( )
(b2+c2-a2),则∠B=( )
A.90° B.60° C.45° D.30°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:解答题
(1)用数学归纳法证明等式1+2+3+…+(n+3)=  .
.
(2)用数学归纳法证明不等式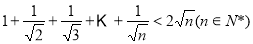 .
.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
设m∈N*,且m<15,则(15-m)(16-m)…(20-m)等于( )
A. B.
B. C.
C.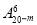 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com