
(1)用数学归纳法证明等式1+2+3+…+(n+3)=  .
.
(2)用数学归纳法证明不等式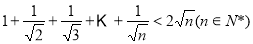 .
.
见解析
【解析】
试题分析:本题考查用数学归纳法证明等式成立,用数学归纳法证明问题的步骤是:第一步验证当n=n0时命题成立,第二步假设当n=k时命题成立,那么再证明当n=k+1时命题也成立.本题解题的关键是利用第二步假设中结论证明当n=k+1时成立
试题解析:证明:(1)①当n=1时,左边=1+2+3+4=10,右边=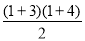

左边=右边.
②假设n=k时等式成立,即1+2+3+…+(k+3)=
那么n=k+1时,等式左边=1+2+3+…+(k+3)+(k+4)=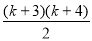 +(k+4)
+(k+4)
=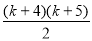
等式成立.
综上1+2+3+…+(n+3)=  成立.
成立.
(2)证明:①当n=1时,左边=1,右边=2,∴n=1不等式成立.
②假设当n=k(k≥2)时成立,即
那么当n=k+1时,左边=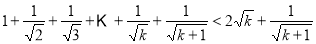
∵4k2+4k<4k2+4k+1,可得
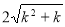
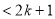 ,
,
即: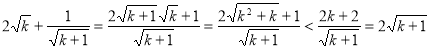
.这就是说n=k+1时不等式也成立.
综上①②可知不等式对所有的n∈N*
考点:数学归纳法证明不等式


科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:选择题
下列程序语言中,哪一个是输入语句( )
A.PRINT B.INPUT C.THEN D.END
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一次检查文科数学试卷(解析版) 题型:选择题
已知数列{a }的前n项和
}的前n项和 满足:
满足: ,且
,且 =1.那么
=1.那么 =( )
=( )
A.1 B.9 C.10 D.55
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:解答题
设函数 .
.
(1)当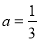 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)在(1)的条件下,设函数 ,若对于
,若对于 ,
,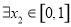 ,使
,使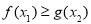 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:填空题
a,b∈R,a+bi=(1+2i)(1-i)(i为虚数单位),则a+b的值为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:选择题
已知各项均为正数的等比数列{an}中, a1a2a3=5,a7a8a9=10,则a4a5a6= ( )
A.5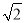 B.7 C.6 D.4
B.7 C.6 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高一上学期10月月考数学试卷(解析版) 题型:选择题
下列函数中,既是奇函数,又是定义域上单调递减的函数为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com