
已知函数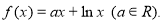
(1)若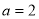 ,求曲线
,求曲线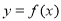 在
在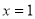 处的切线方程;
处的切线方程;
(2)求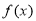 的单调区间;
的单调区间;
(3)设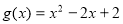 ,若对任意
,若对任意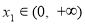 ,均存在
,均存在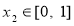 ,使得
,使得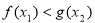 ,求
,求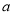 的取值范围.
的取值范围.
(1)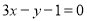 (2)详见解析(3)
(2)详见解析(3)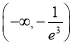
【解析】
试题分析:
(1)已知函数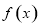 的解析式,把切点的横坐标带入函数
的解析式,把切点的横坐标带入函数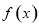 即可求出切点的纵坐标,对
即可求出切点的纵坐标,对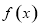 求导得到函数
求导得到函数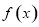 的导函数
的导函数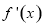 ,把
,把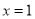 带入导函数
带入导函数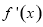 即可求的切线的斜率,利用点斜式即可得到切线的方程.
即可求的切线的斜率,利用点斜式即可得到切线的方程.
(2)对函数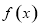 进行求导和求定义域,导函数
进行求导和求定义域,导函数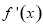 喊参数
喊参数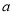 ,把
,把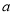 分为两种情况进行讨论,首先
分为两种情况进行讨论,首先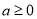 时,结合
时,结合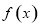 的定义域
的定义域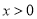 即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当
即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当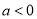 时,求解导函数
时,求解导函数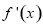 大于0和小于0的解集,得到原函数的单调递增和单调递减区间.
大于0和小于0的解集,得到原函数的单调递增和单调递减区间.
(3)该问题为存在性问题与恒成立问题的结合,即要求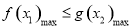 ,而
,而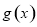 的最大值可以利用二次函数
的最大值可以利用二次函数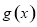 的图像得到函数
的图像得到函数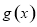 在区间
在区间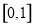 上的最值,函数
上的最值,函数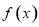 的最大值可以利用第二问的单调性求的,当
的最大值可以利用第二问的单调性求的,当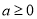 时,函数
时,函数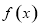 单调递增,无最大值,故不符合题意,当
单调递增,无最大值,故不符合题意,当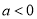 时,函数
时,函数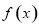 在
在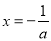 处前的最大值,带入不等式即可求的
处前的最大值,带入不等式即可求的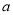 的取值范围.
的取值范围.
试题解析:
(1)由已知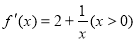 , 1分
, 1分
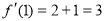 ,所以斜率
,所以斜率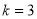 , 2分
, 2分
又切点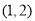 ,所以切线方程为
,所以切线方程为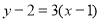 ),即
),即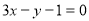
故曲线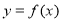 在
在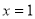 处切线的切线方程为
处切线的切线方程为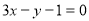 。 3分
。 3分
(2)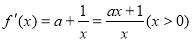 4分
4分
①当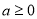 时,由于
时,由于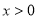 ,故
,故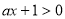 ,
,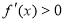 ,所以
,所以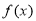 的单调递增区间为
的单调递增区间为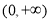 .
.
5分
②当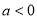 时,由
时,由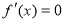 ,得
,得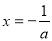 . 6分
. 6分
在区间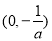 上,
上,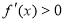 ,在区间
,在区间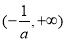 上,
上,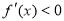 ,
,
所以,函数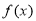 的单调递增区间为
的单调递增区间为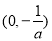 ,单调递减区间为
,单调递减区间为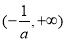 . 7分
. 7分
(3)由已知,转化为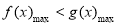 . 8分
. 8分
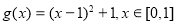 ,所以
,所以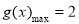 9分
9分
由(2)知,当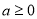 时,
时,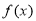 在
在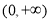 上单调递增,值域为
上单调递增,值域为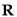 ,故不符合题意.
,故不符合题意.
(或者举出反例:存在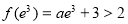 ,故不符合题意.) 10分
,故不符合题意.) 10分
当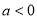 时,
时,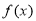 在
在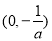 上单调递增,在
上单调递增,在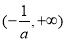 上单调递减,
上单调递减,
故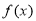 的极大值即为最大值,
的极大值即为最大值,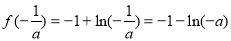 , 12分
, 12分
所以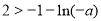 ,解得
,解得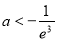 . 14分
. 14分
考点:恒成立问题存在性问题导数切线


科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:选择题
定义一个集合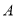 的所有子集组成的集合叫做集合
的所有子集组成的集合叫做集合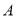 的幂集,记为
的幂集,记为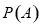 ,用
,用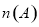 表示有限集
表示有限集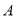 的元素个数,给出下列命题:①对于任意集合
的元素个数,给出下列命题:①对于任意集合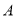 ,都有
,都有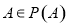 ;②存在集合
;②存在集合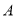 ,使得
,使得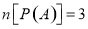 ;
;
③用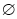 表示空集,若
表示空集,若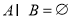 ,则
,则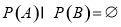 ;④若
;④若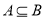 ,则
,则 ;⑤若
;⑤若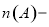
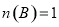 ,则
,则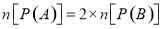 其中正确的命题个数为( )
其中正确的命题个数为( )
A.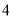 B.
B.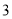 C.
C.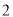 D.
D.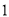
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:填空题
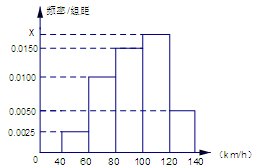
根据某固定测速点测得的某时段内过往的 辆机动车的行驶速度(单位:
辆机动车的行驶速度(单位: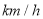 )绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为
)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为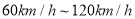 ,则该时段内过往的这
,则该时段内过往的这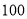 辆机动车中属非正常行驶的有辆,图中的
辆机动车中属非正常行驶的有辆,图中的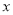 值为.
值为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:选择题
如图所示的程序框图,能使输入的 值与输出的
值与输出的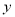 值相等的
值相等的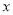 值分别为( )
值分别为( )
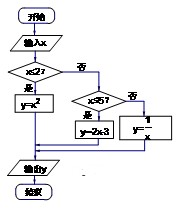
A.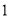 、
、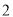 、
、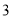 B.
B.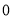 、
、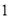 C.
C.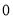 、
、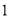 、
、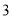 D.
D.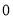 、
、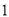 、
、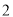 、
、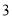 、
、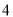
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
已知 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, .设函数
.设函数 ,当
,当 时,函数
时,函数 的值域为集合
的值域为集合 ,则
,则 中的元素个数为.
中的元素个数为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
(坐标系与参数方程选做题)在极坐标系中,直线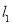 的方程是
的方程是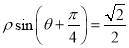 ,以极点为原
,以极点为原
点,以极轴为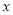 轴的正半轴建立直角坐标系,在直角坐标系中,直线
轴的正半轴建立直角坐标系,在直角坐标系中,直线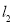 的方程是
的方程是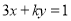 .如果直线
.如果直线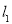 与
与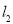
垂直,则常数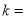 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com