
A. | B. | C. | D. |
科目:高中数学 来源:不详 题型:解答题
 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为 。
。 。
。 ,求
,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个人,以研究这一社区居民在
个人,以研究这一社区居民在 时间段的休闲方
时间段的休闲方| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 |  |  | 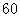 |
| 女 |  |  |  |
| 合计 |  | 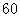 |  |
 名在该社区的男性,设调查的
名在该社区的男性,设调查的 人
人 ,求
,求 的分布列和期望;
的分布列和期望; %的把握认为“在
%的把握认为“在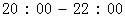 时间段的休闲方式与
时间段的休闲方式与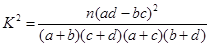 ,其中
,其中 .
. |  |  |  | 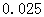 |  |
 |  |  |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 刚好是边长为
刚好是边长为 的等边三角形的三个顶点.
的等边三角形的三个顶点. 区域射击(不会打到
区域射击(不会打到 外),则此次射击的着弹点距
外),则此次射击的着弹点距 的距离都超过
的距离都超过 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计) 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间 内.现从这
内.现从这 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为 和
和 )进行技术分析.求事件“
)进行技术分析.求事件“ ”的概率.
”的概率. 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
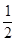 、
、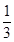 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为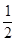 ,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =(m,n),
=(m,n), =(3,6),则向量
=(3,6),则向量 与
与 共线的概率为[
共线的概率为[ 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com