
 个人,以研究这一社区居民在
个人,以研究这一社区居民在 时间段的休闲方
时间段的休闲方| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 |  |  | 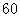 |
| 女 |  |  |  |
| 合计 |  | 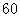 |  |
 名在该社区的男性,设调查的
名在该社区的男性,设调查的 人
人 ,求
,求 的分布列和期望;
的分布列和期望; %的把握认为“在
%的把握认为“在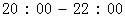 时间段的休闲方式与
时间段的休闲方式与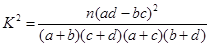 ,其中
,其中 .
. |  |  |  | 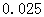 |  |
 |  |  |  |  |  |
科目:高中数学 来源:不详 题型:单选题
| A.“至少有1名女生”与“都是女生” | B.“至少有1名女生”与“至多1名女生” |
| C.“至少有1名男生”与“都是女生” | D.“恰有1名女生”与“恰有2名女生” |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
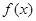 =
=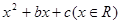 。
。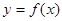 有零点的概率;
有零点的概率;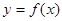 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取
个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取 球.获奖规则如下:依次取到标有“生”“意”“兴”
球.获奖规则如下:依次取到标有“生”“意”“兴” “隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖. (Ⅱ)设摸球次数为
(Ⅱ)设摸球次数为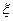 ,求
,求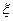 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com