
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 18 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 36 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| ζ | 10 | 30 | 50 | ||||||
| P |
|
|
|
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 100 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 18 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 36 |
| η | 10 | 30 | 50 | 70 | 90 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 18 |
| 1 |
| 12 |
| 1 |
| 36 |
| 235 |
| 9 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知某车站每天8:00―9:00、9:00―10:00都恰好有一辆客车到站;8:00―9:00到站的客车![]() 可能在8:10、8:30、8:50到,其概率依次为
可能在8:10、8:30、8:50到,其概率依次为![]() .9:00―10:00到站的客车
.9:00―10:00到站的客车![]() 可能在9:10、9:30、9:50到,其概率依次为
可能在9:10、9:30、9:50到,其概率依次为![]() .今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
.今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省六校高三(上)第一次联考数学试卷(理科)(解析版) 题型:解答题
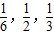 ;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为
;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为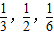 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省岳阳一中高二(下)数学综合练习试卷7(解析版) 题型:解答题
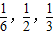 ;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为
;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为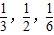 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com